《Node》

《算法与数据结构:Node》
节点(Node)数据结构基石
理解 Node 数据结构及其应用
Node(节点)在计算机科学中扮演着核心角色,它是构建更复杂数据结构的基石。深入理解 Node 及其在各种数据结构中的应用,对于开发高效、可扩展的软件应用至关重要。
Node 节点概念
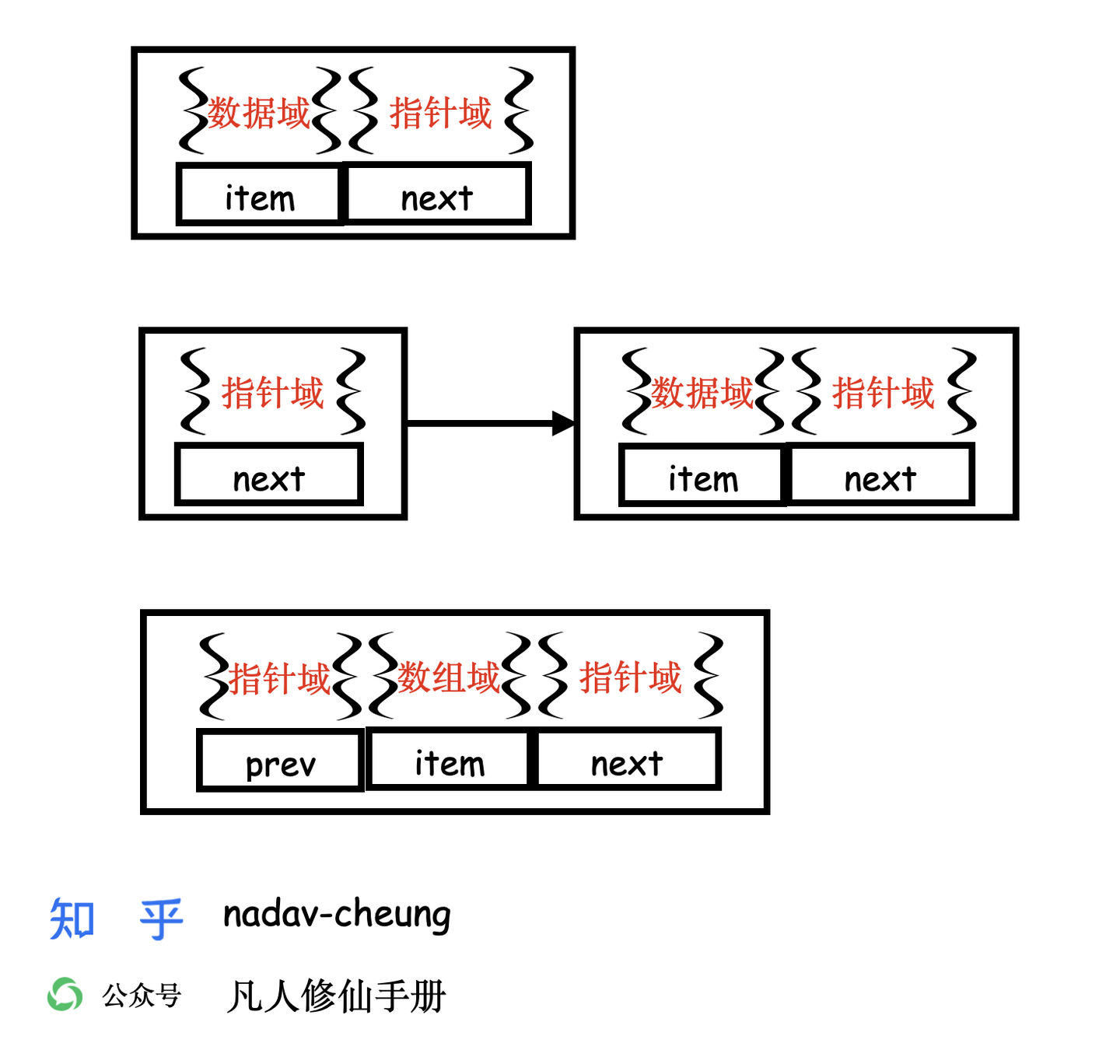
- 定义与结构:Node 通常是一个包含数据和指向其他节点的引用的对象。它的结构可能因应用的不同而有所不同,但通常包括至少一个数据字段和一个或多个链接字段。
- 类型:
- 单链表节点:包含数据和指向下一个节点的单个链接。
- 双链表节点:除了指向下一个节点的链接外,还有指向前一个节点的链接。
- 树节点:包含多个链接,通常指向其子节点。
- 图节点:可以有多个链接,指向多个其他节点,表示图中的边。
Node 在数据结构中的应用
- 链表(Linked Lists):在链表中,每个节点包含数据和指向下一个节点的引用。链表可以是单向的(每个节点只有一个指向下一个节点的链接)或双向的(每个节点有两个链接,分别指向前一个节点和下一个节点)。链表的优势在于它可以高效地在任何位置添加或删除节点。
- 树(Trees):在树形结构中,每个节点包含数据和几个指向子节点的链接。树的一个常见例子是二叉树,其中每个节点最多有两个子节点。树被广泛用于表示具有层次结构的数据,例如文件系统。
- 图(Graphs):图是由节点(在图中称为顶点)和边组成的数据结构。每个边连接两个节点。图可以用来表示网络,如社交网络或交通网络。
- 堆(Heaps):堆是一种特殊的树形结构,用于实现优先队列。在堆中,节点的排列方式依赖于它们的键值,以保证对堆顶(根节点)的快速访问。
- 散列表(Hash Tables):虽然散列表通常不直接展示其节点,但它们内部使用节点来存储键值对。散列函数决定了键应该存储在哪个节点中。
- 链表
- 类型:
- 单向链表
- 双向链表
- 循环链表
- 操作:
- 插入:在链表的特定位置插入新节点。
- 删除:移除特定节点。
- 搜索:查找具有特定值的节点。
- 应用:栈、队列的实现,动态内存分配。
- 类型:
- 树
- 类型:
- 二叉树
- 平衡树(如 AVL 树)
- B 树及其变种
- 操作:
- 插入:在树中加入新节点。
- 删除:移除树中的节点。
- 遍历:按顺序访问树中的每个节点(前序、中序、后序)。
- 应用:数据库索引,文件系统。
- 类型:
- 图
- 类型:
- 有向图
- 无向图
- 操作:
- 添加边:连接两个节点。
- 删除边:移除两个节点间的连接。
- 遍历:例如深度优先搜索(DFS)或广度优先搜索(BFS)。
- 应用:社交网络分析,路由算法。
- 类型:
Node 的 Java 版本实现
详细实现示例:
链表节点实现:1
2
3
4
5
6
7
8class ListNode<E> {
E data;
ListNode<E> next;
public ListNode(E data) {
this.data = data;
this.next = null;
}
}
二叉树节点实现:1
2
3
4
5
6
7
8
9
10
11class TreeNode<E> {
E data;
TreeNode<E> left;
TreeNode<E> right;
public TreeNode(E data) {
this.data = data;
this.left = null;
this.right = null;
}
}
图节点实现:1
2
3
4
5
6
7
8
9class GraphNode<E> {
E data;
List<GraphNode<E>> neighbors;
public GraphNode(E data) {
this.data = data;
this.neighbors = new ArrayList<>();
}
}
Node 的重要性和高级应用
- 高级算法中的应用:
- 排序算法:例如归并排序在链表上的应用。
- 动态编程问题:使用树结构存储中间结果。
- 网络算法:使用图结构模拟和解决网络路由和连接问题。
- 性能考量:
- 时间复杂度:不同结构的节点操作具有不同的时间复杂度,如链表的插入操作通常是 O (1),而数组则是 O (n)。
- 空间复杂度:节点结构对内存的使用效率也有重要影响。
链表
单向链表图解
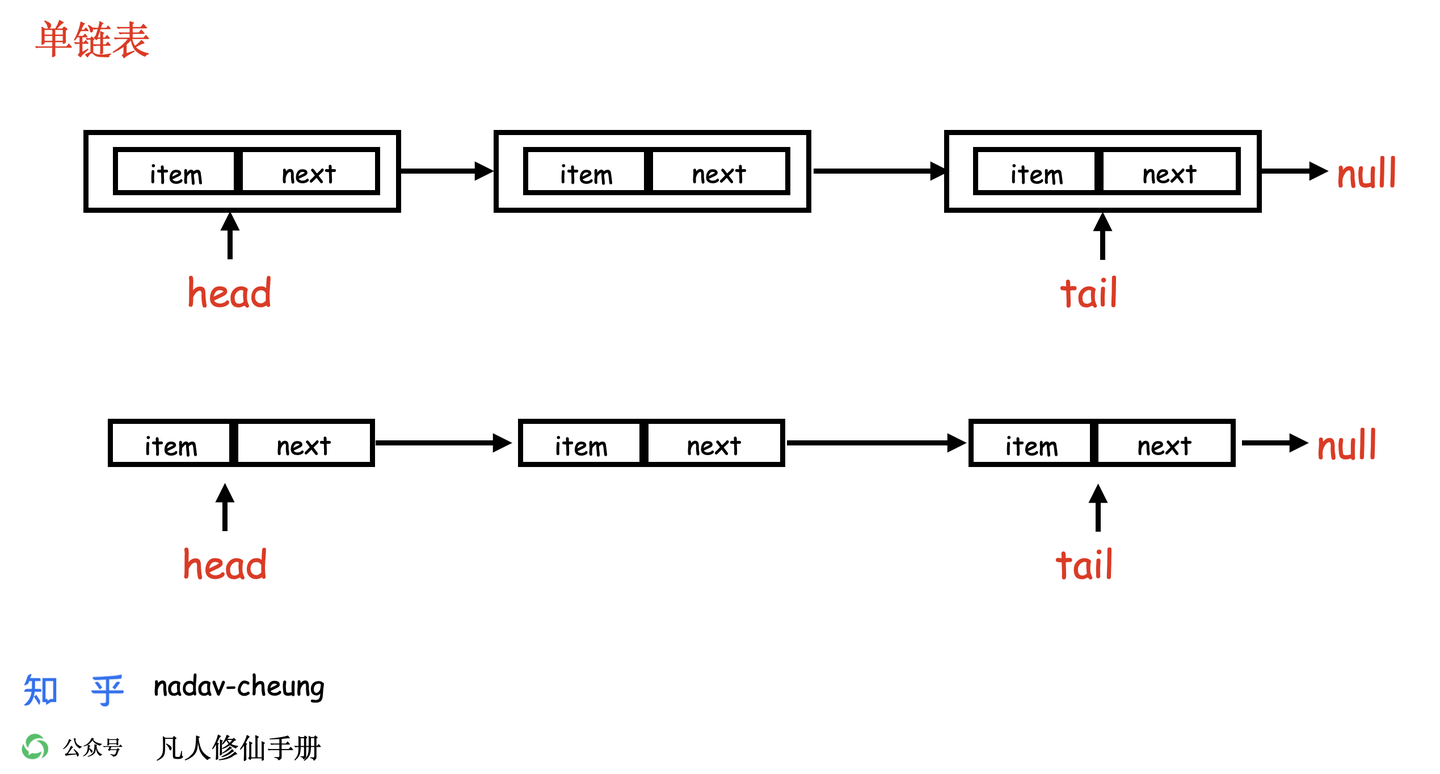
单向链表遍历
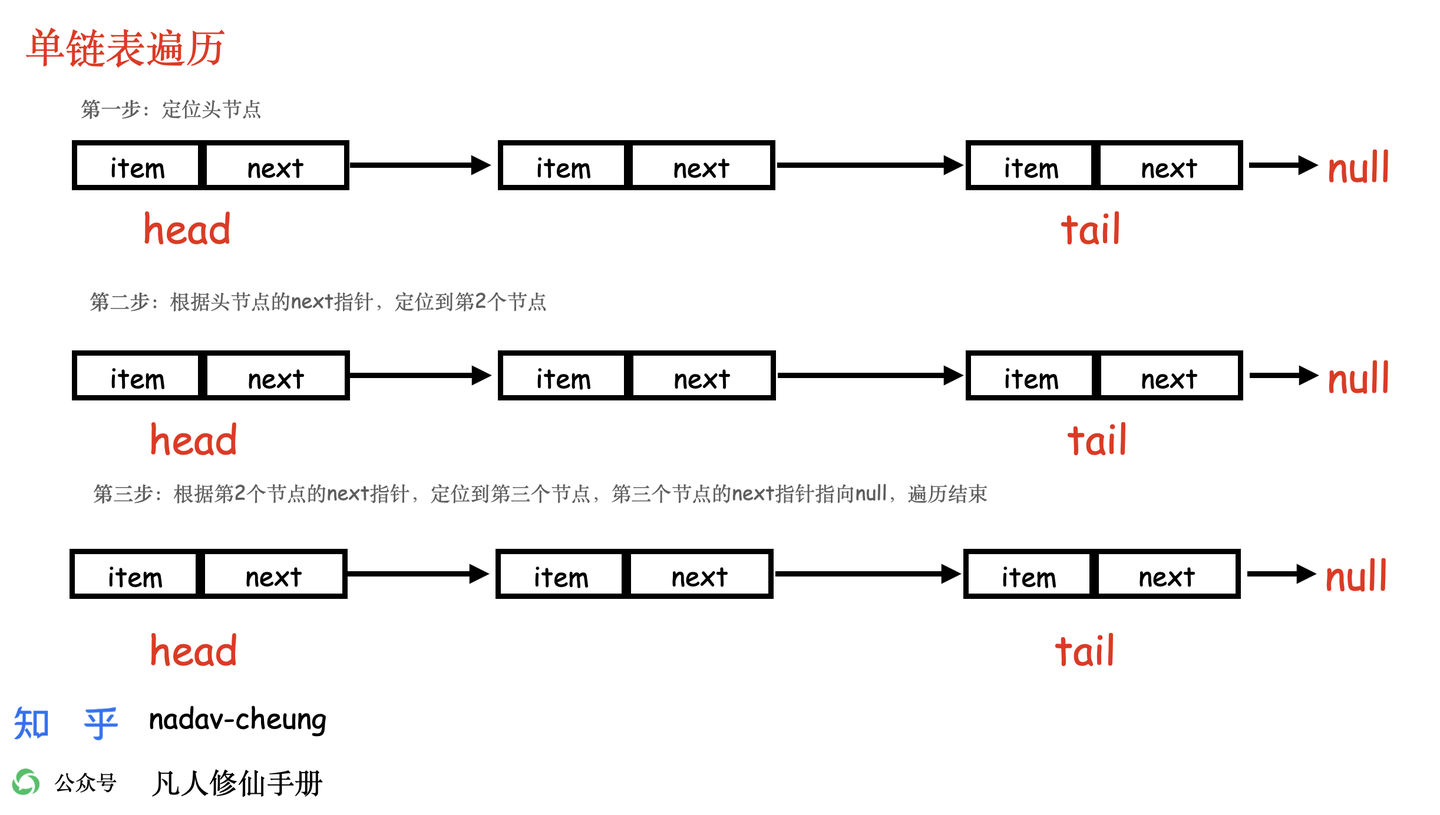
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18链表遍历
class ListNode{
int val;
ListNode next;
}
//迭代
void traverse(ListNode head) {
for(ListNode p = head; p!=null; p = p.next){
// p.val
}
}
//递归
void traverse(ListNode head){
// 递归 head.val;
traverse(head.next);
}
单向链表遍历实战
todo queue 队列的实现
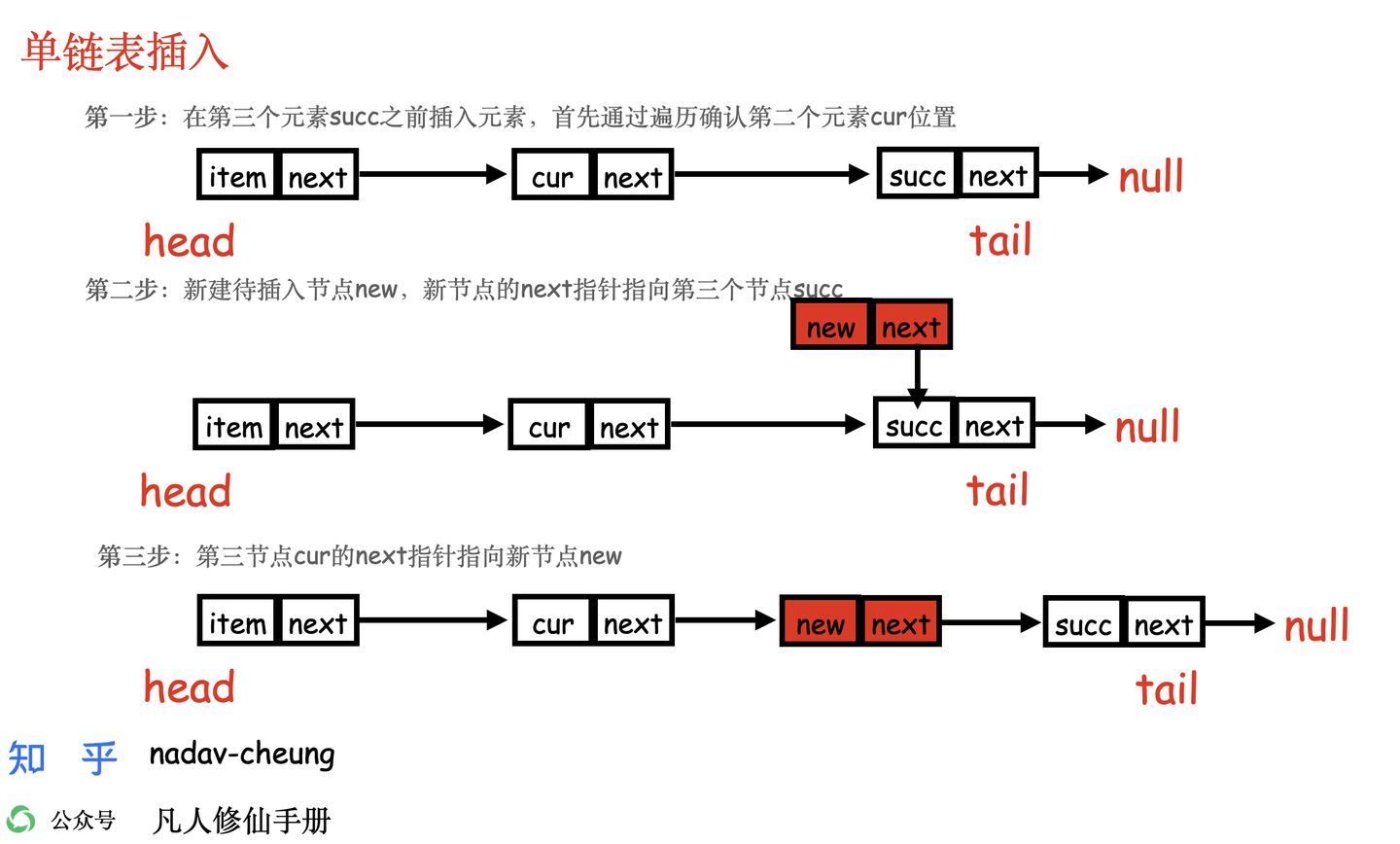
单向链表插入
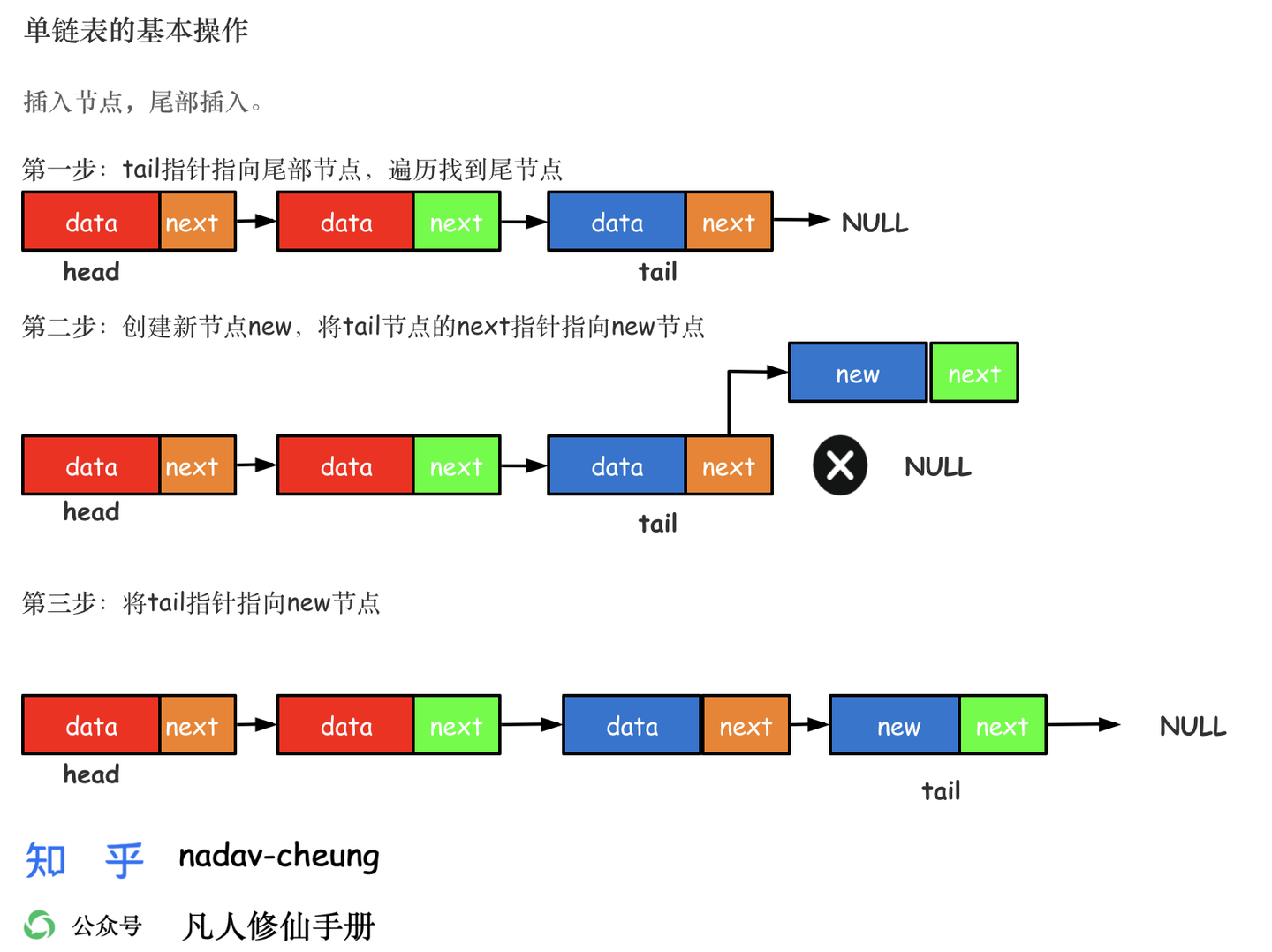
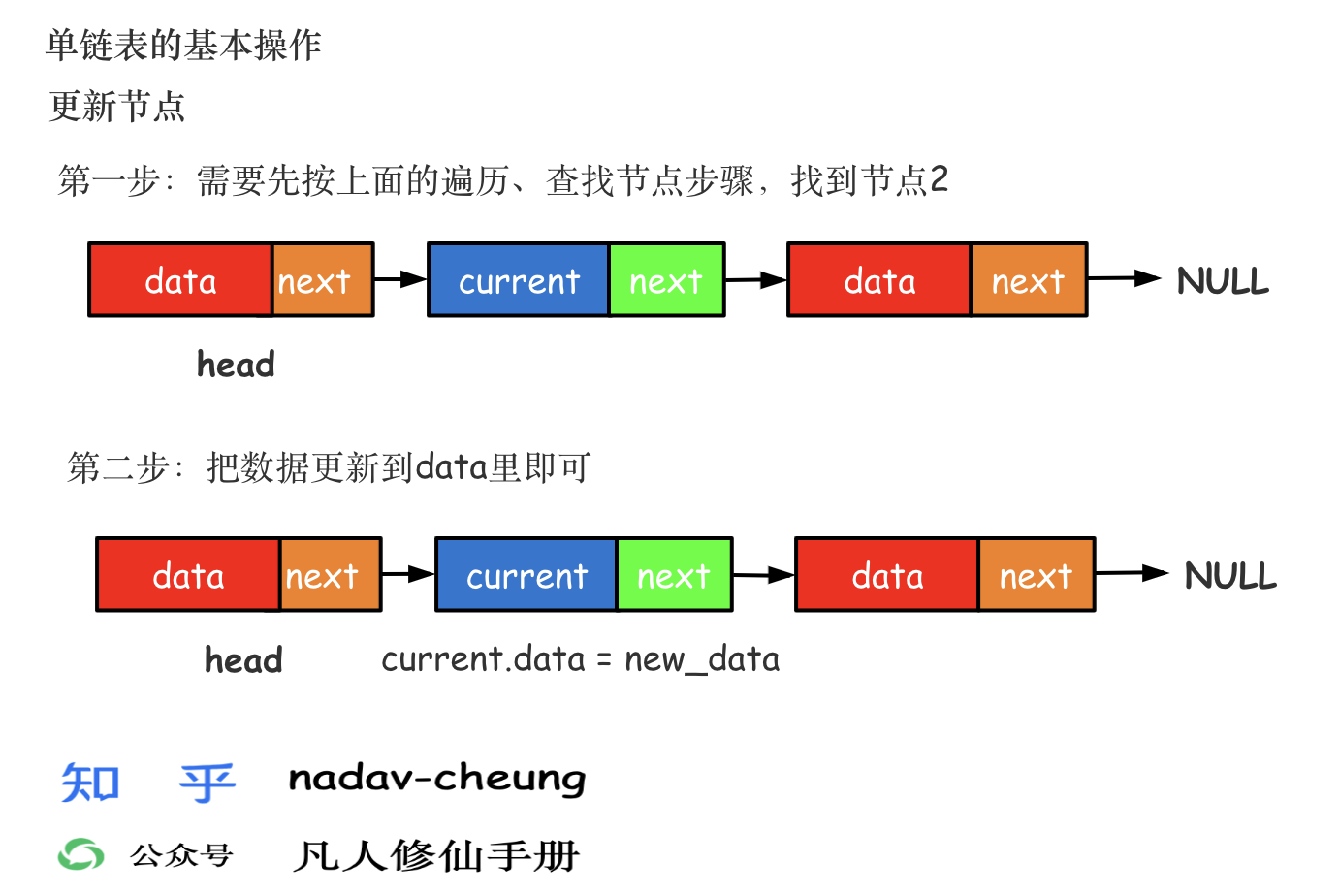
单向链表更新
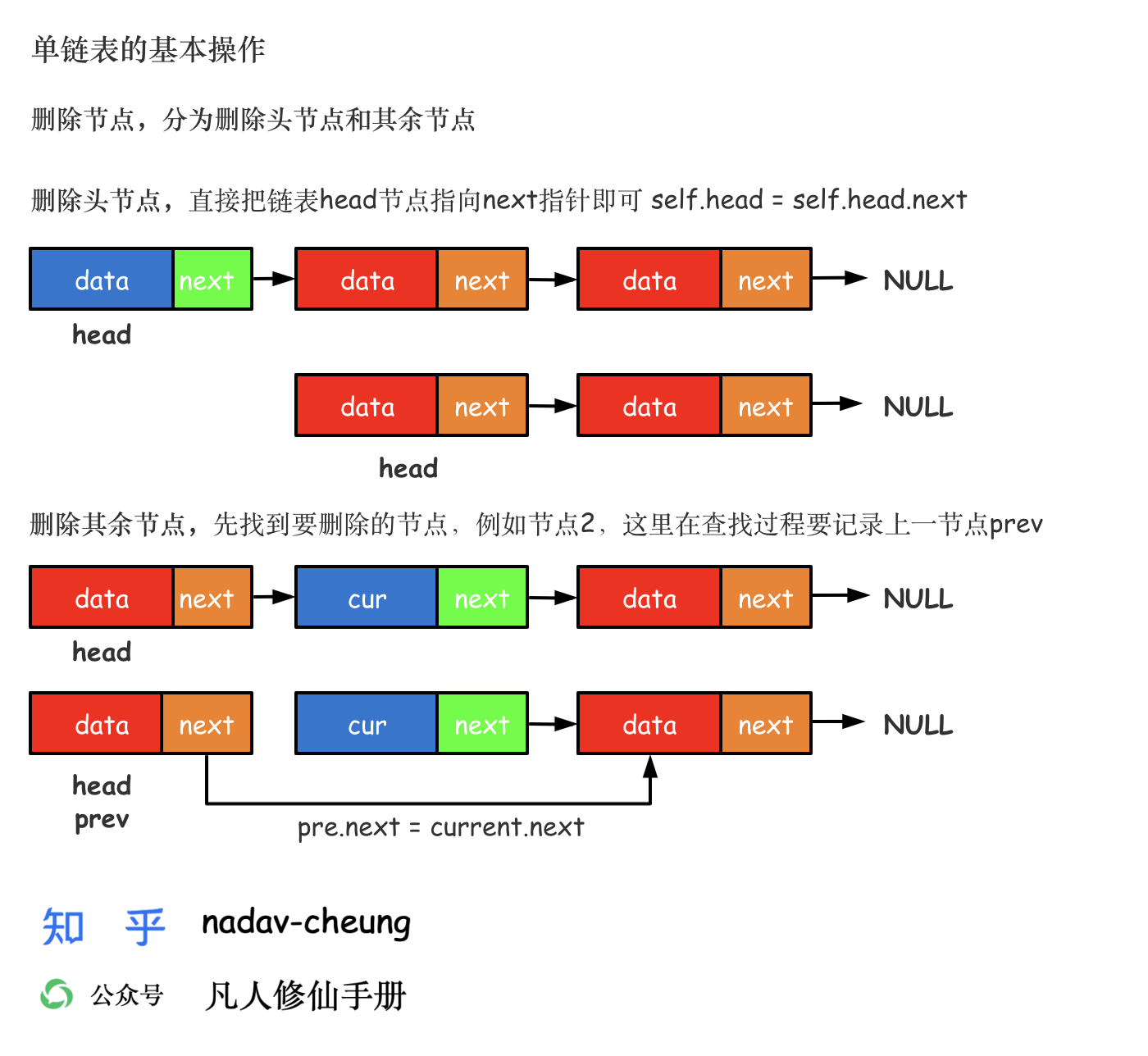
单向链表删除
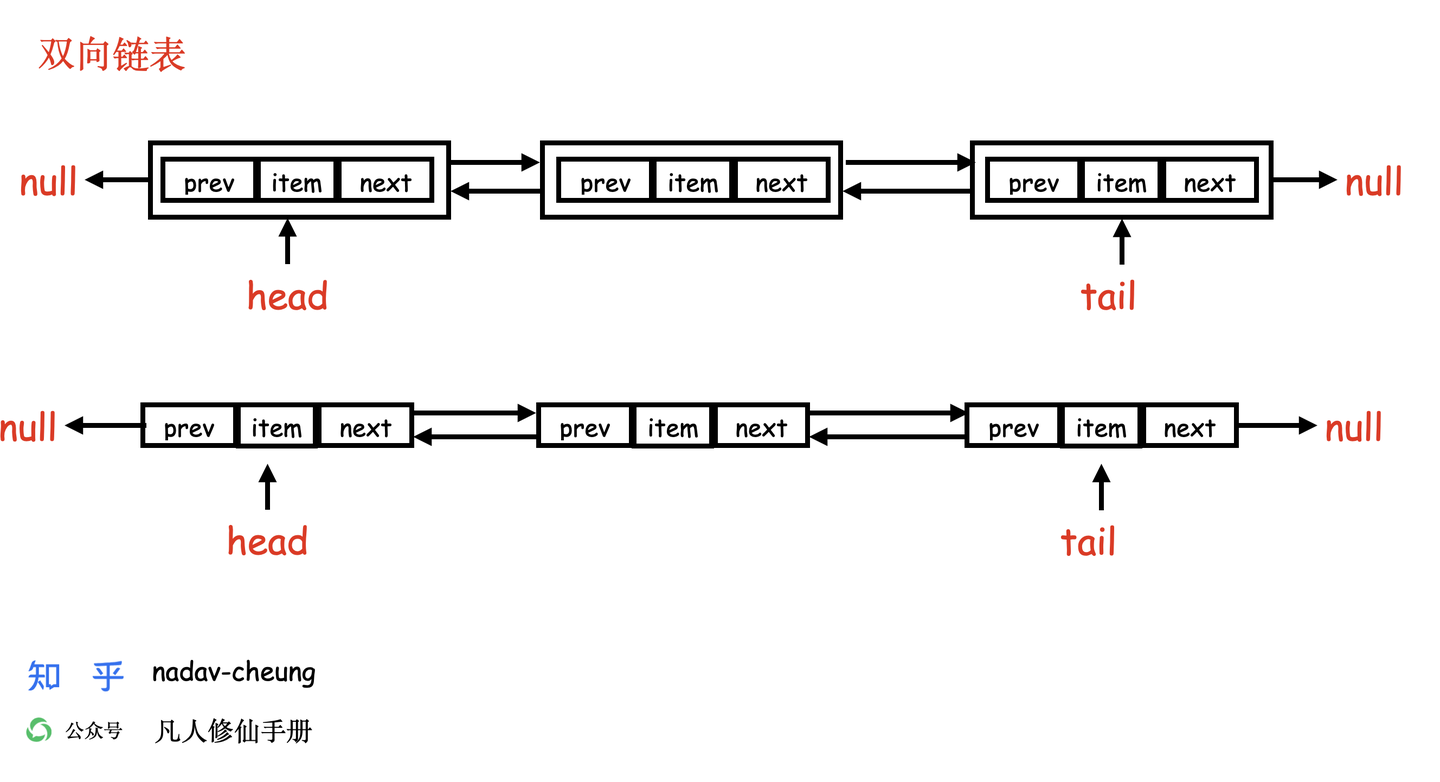
双向链表图解
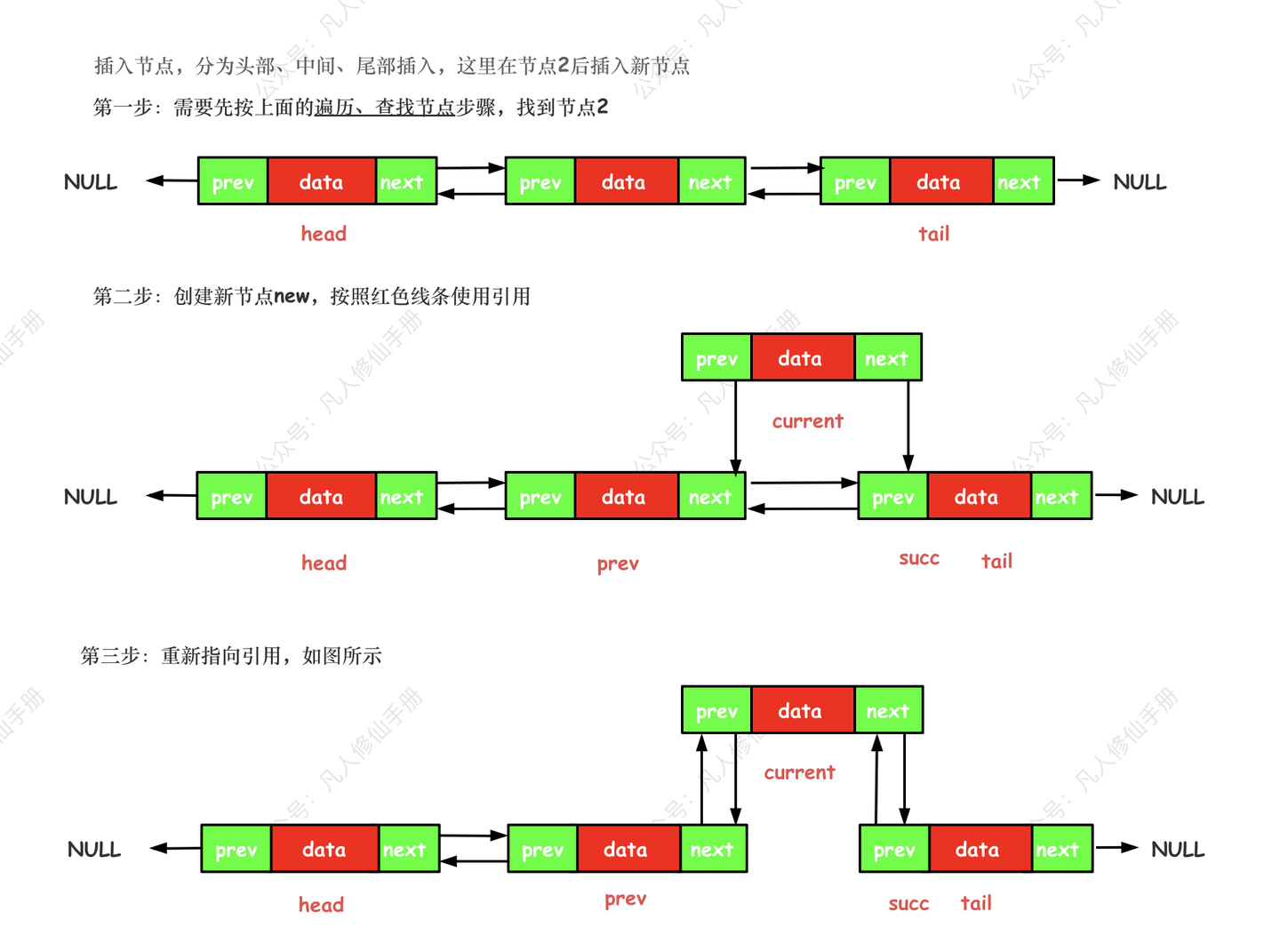
双向链表新增元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28// 双向链表
static class Node<E> {
E item;
Node<E> prev;
Node<E> next;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
/**
* Inserts element e before non-null Node succ.
*/
void linkBefore(E e, Node<E> succ) {
// assert succ != null;
final Node<E> pred = succ.prev;
final Node<E> newNode = new Node<>(pred, e, succ);
succ.prev = newNode;
if (pred == null)
first = newNode;
else
pred.next = newNode;
size++;
}
字典树
BST 树
todo
AVL 树
todo