《[04] 寻找两个正序数组的中位数》

发表于 分类于 阅读次数： 本文字数： 1.5k 阅读时长 ≈ 6 分钟
个人公众号

《LeetCode:[04] 寻找两个正序数组的中位数》

《LeetCode：[04]寻找两个正序数组的中位数》

力扣（LeetCode）官网 - 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O (log (m+n)) 。

示例 1：

1
2
3
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

1
2
3
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

方法签名

1
2
public double findMedianSortedArrays(int[] nums1, int[] nums2) {  
}

解题思路历程

看完这个问题你想到了什么？若是思路没有问题应该是二分搜索算法，但传统的二分搜索是针对一个已经排序的数组，但这里有两个已经排序的数组，那应该怎么处理呢？

最直观的思路：将两个已排序的数组合并为一个已经排序的数组，然后使用二分搜索算法搜索结果。

img

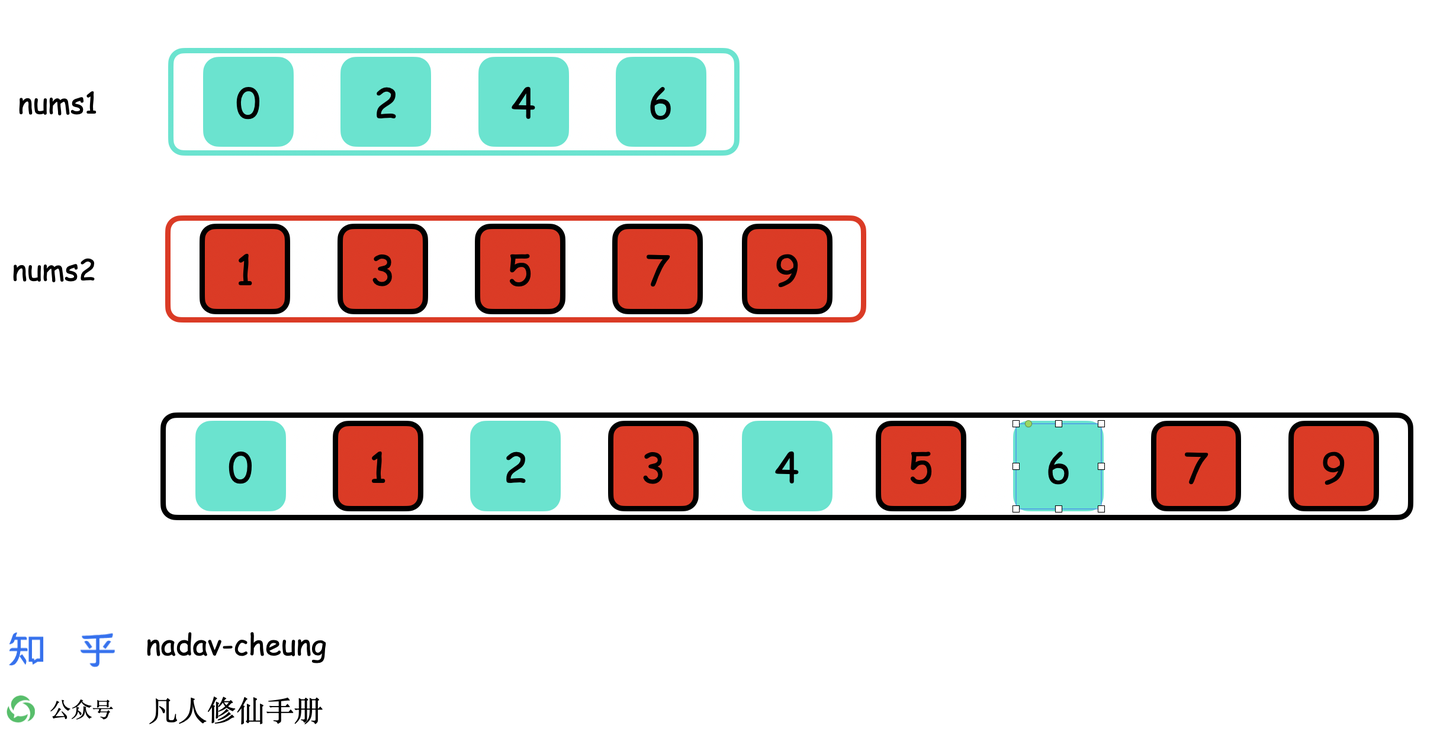
将两个排序数组合并为一个排序数组

可以非常明显的看出答案是 4，但是两个有序数组合并的时间复杂度 O(m+n)，已经不符合 O(log (m+n)) 的要求。

那么如何在不合并的情况下找出这个结果呢？我们找一下规律，其实就是 nums1 数组中有一个 i 将数组 nums1 分成两半， nums2 数组中有一个 j 将数组 nums2 分成两半。数组 nums1 和 nums2 的前一半数量等于两个数组数量和（m+n）的一半，结果向上取整。 数组 nums1 和 nums2 的前一半数据的最大值小于等于后一半数据的最小值。

img

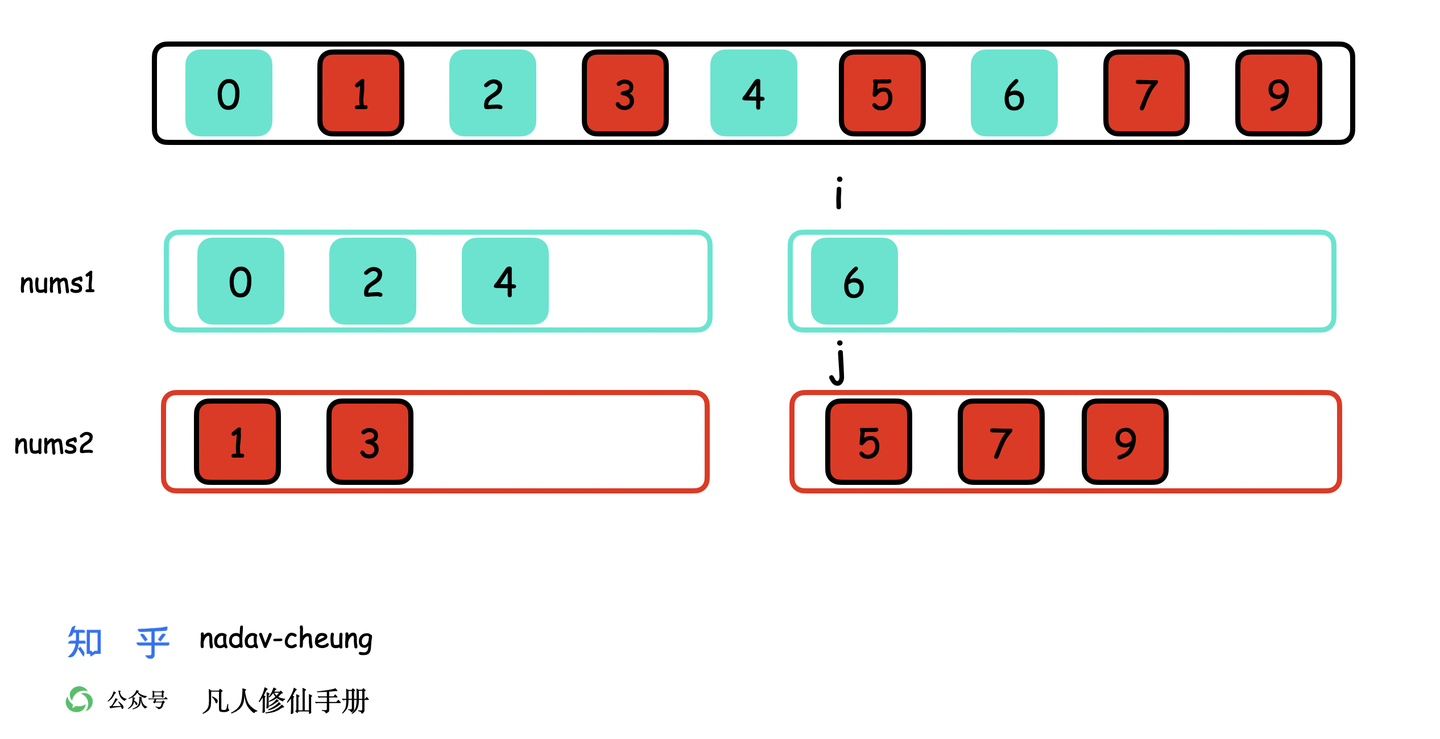
i 和 j 切分后的数组

我们将合并后的数组重新拆开，发现一个规律，只要找到一个合适的 **i** 和 **j** 满足以下情况，如上图。
$$
i+j=（m+n+1）/2
$$

$$
nums1[i-1]<=nums2[j]
$$

$$
nums[j-1]<=nums1[i]
$$

最终，这个问题就可以转换成在较小的那个数组上进行二分查找，需要找出一个 **i** 满足如下条件。
$$
j=（m+n+1）/2 -i
$$

$$
nums1[i-1]<=nums2[j]
$$

$$
nums[j-1]<=nums1[i]
$$

解题步骤：

理解问题:

  • 目标是找到两个已排序数组的中位数。
  • 假设数组 nums1 和 nums2 都不为空，并且它们的总长度是 m+n。

检查特殊情况:

  • 如果一个数组为空，中位数就是另一个数组的中位数。
  • 如果两个数组的总长度是偶数，中位数是中间两个数的平均值；如果是奇数，则是中间的那个数。

二分搜索法:

  • 使用二分搜索找到合适的切分位置。这意味着在 nums1 和 nums2 中找到两个位置 i 和 j，使得
    $$
    nums1[i-1]<=nums2[j]
    $$

    $$
    nums1[i-1]<=nums2[j]
    $$

  • 这个过程需要不断调整 i 和 j 以满足上述条件，同时保证

$$
i+j=（m+n+1）/2
$$

计算中位数:

  • 一旦找到合适的 i 和 j，中位数可以通过比较

  • nums1 [i-1]、nums1 [i]、nums2 [j-1] 和 nums2 [j] 来确定。

  • 如果总长度是奇数，则中位数是
    $$
    max(nums1[i-1],nums2[j-1])
    $$

  • 如果总长度是偶数，则中位数是

$$
(max(nums1[i-1],nums[j-1])+max(nums1[i],nums[j]))/2
$$

边界条件处理:

  • 在二分搜索过程中，需要考虑数组边界情况。
  • 例如，当 i 为 0 或 n 时，应该相应地处理 nums1[i-1] 或 nums1[i]。

时间复杂度分析:

此算法的时间复杂度通常是 O(log(min(m, n)))，其中 m 和 n 是两个数组的长度。

实现这个算法时，关键在于理解如何通过二分搜索在两个数组中找到正确的切分点，以及如何处理边界情况。

解题步骤

选择较短的数组进行二分查找：为了优化性能，总是在两个数组中较短的那个上执行二分查找。

二分查找的应用：使用二分查找找到一个切分点，这个切分点将两个数组划分为左右两部分，使得左边所有元素都小于右边的所有元素。

确保切分的正确性：确保左侧部分的最大值小于或等于右侧部分的最小值。

计算中位数：

  • 如果两个数组的总长度是偶数，中位数是左侧最大值和右侧最小值的平均数。
  • 如果总长度是奇数，中位数是左侧的最大值。

处理边界条件：考虑数组长度为零或者切分点在数组的起始或结束位置的情况。

Java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public double findMedianSortedArray(int[] nums1, int[] nums2) {
    // 确保 nums1 是较短的数组
    if (nums1.length > nums2.length) {
        int[] temp = nums1;
        nums1 = nums2;
        nums2 = temp;
        temp = null;  // help gc
    }

    int m = nums1.length;
    int n = nums2.length;
    int left = 0;
    int right = m;
    int halfLength = (m + n + 1) / 2;

    // nums1[i-1] <= nums2[j]
    // nums2[j-1] <= nums1[i]
    // i + j = (n + 1) / 2

    while (left < right) {
        // 两个队列的临时变量
        int i = left + (right - left) / 2;
        int j = halfLength - i;

        if (i < right && nums2[j - 1] > nums1[i]) {
            left = i + 1; // i is too small
        } else if (i >= left && nums1[i - 1] > nums2[j]) {
            right = i; // i is too big
        } else { // i is perfect
            int maxLeft = 0;
            if (i == 0) {
                maxLeft = nums2[j - 1];
            } else if (j == 0) {
                maxLeft = nums1[i - 1];
            } else {
                maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
            }

            if ((m + n) % 2 == 1) {
                return maxLeft;
            }

            int minRight = 0;
            if (i == m) {
                minRight = nums2[j];
            } else if (j == n) {
                minRight = nums1[i];
            } else {
                minRight = Math.min(nums2[j], nums1[i]);
            }
            return (maxLeft + minRight) / 2.0;
        }
    }
    return 0.0;
}

在这个实现中，我们首先确定两个数组中较短的那个，并在其上执行二分查找。

我们不断地调整切分位置，直到找到一个位置，使得左侧所有元素都小于或等于右侧所有元素。然后根据左右两侧元素的最大值和最小值计算出中位数。

这种方法的时间复杂度为 O(log(min(m, n)))，其中 m 和 n 分别是两个数组的长度。