《二分搜索算法》

发表于 分类于 ， 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 9 分钟
个人公众号

《算法与数据结构：二分搜索算法》

简介

二分搜索算法是一种在有序数组中查找特定元素的有效方法。其基本思想是通过将搜索区间分成两半，然后根据目标值与中间元素的比较结果来选择搜索的半区，从而逐步缩小搜索范围，直到找到目标值或确定目标值不存在。

二分搜索的工作原理

二分搜索（又称二分查找）是一种在有序数组中查找特定元素的算法。在 Java 中实现二分搜索，你可以遵循以下步骤：

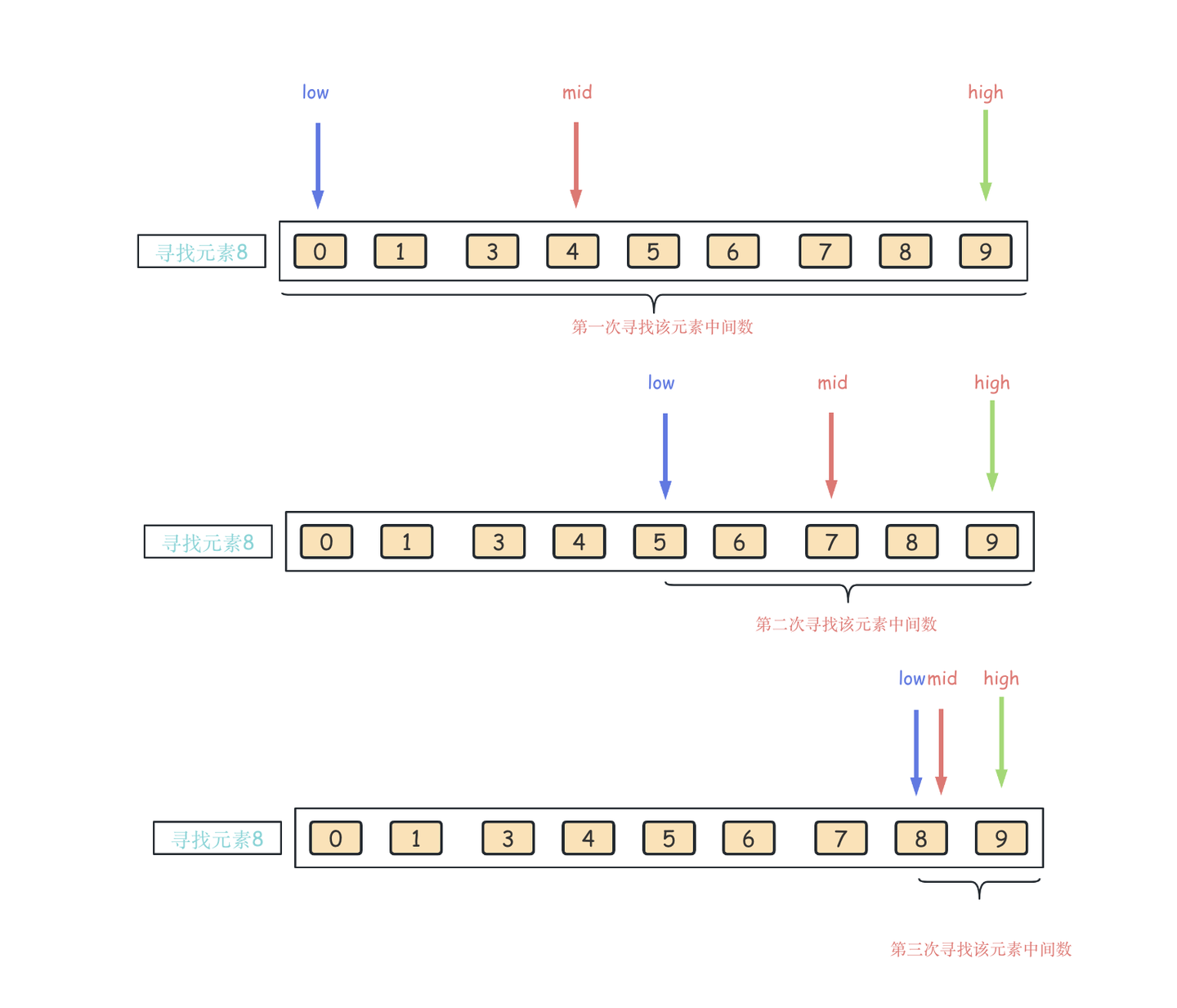
确定查找范围：设置两个指针，low 和 high，分别表示数组的起始和结束位置 nums [low,high) 左闭右开区间。

计算中间位置：在每次迭代中，计算中间位置 mid = low + (high - low) / 2。

比较和移动指针：

  • 如果 arr [mid] 等于目标值，返回 mid。
  • 如果 arr [mid] 小于目标值，说明目标值在数组的右半部分，将 low 更新为 mid + 1。
  • 如果 arr [mid] 大于目标值，说明目标值在数组的左半部分，将 high 更新为 mid。

重复步骤 2 和 3，直到 low 超过 high，表示找不到目标值，返回 -1。

img

二分搜索的优势

  • 效率高：二分搜索的时间复杂度为 O (log n)，远高于线性搜索的 O (n)。
  • 适用范围广：适用于任何可以快速访问元素的有序数组。

Java 二分搜索递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
 /**
 * 二分搜索（又称二分查找）是一种在有序数组中查找特定元素的算法
 *
 * @param array  有序数组
 * @param target 目标数据
 * @return array index 不存在则返回-1
 */
public static int recursionSearch(int[] array, int target) {
    return recursionSearch(array, 0, array.length, target);
}


/**
 * @param array  数组
 * @param l      左边界
 * @param r      右边界 初始化时等于数组长度  array[l,r)左闭右开区间
 * @param target
 * @return
 */
private static int recursionSearch(int[] array, int l, int r, int target) {

    // array[l,r) 在左闭右开区间中寻找 target
    if (l >= r) {
        return -1;
    }
    int mid = l + (r - l) / 2;

    if (array[mid] == target) {
        return mid;
    }

    if (array[mid] < target) {
        return recursionSearch(array, mid + 1, r, target);
    }

    // it means array[mid] > target
    return recursionSearch(array, l, mid, target);
}

二分搜索递归范型实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Java范型接口
public static <E extends Comparable<? super E>> int recursionSearch(E[] array, E target) {
    return recursionSearch(array, 0, array.length, target);
}


public static <E extends Comparable<? super E>> int recursionSearch(E[] array, int l, int r, E target) {
    if (l >= r) {
        return -1;
    }

    int mid = l + (r - l) / 2;

    if (array[mid].compareTo(target) == 0) {
        return mid;
    }

    if (array[mid].compareTo(target) < 0) {
        return recursionSearch(array, mid + 1, r, target);
    }

    return recursionSearch(array, l, mid, target);
}

二分搜索迭代实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
   * 迭代实现
   */
  public static int iterationSearch(int[] array, int target) {
      int l = 0;
      int r = array.length;
      // 在 array[l,r）中寻找target
      while (l < r) {
          int mid = l + (r - l) / 2;
          if (array[mid] == target) {
              return mid;
          } else if (array[mid] < target) {
              l = mid + 1;
          } else if (array[mid] > target) {
              r = mid;
          }
      }
      return -1;
  }


二分搜索迭代范型实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static <E extends Comparable<? super E>> int iterationSearch(E[] array, E target) {
    int l = 0;
    int r = array.length;

    // 在 array[l,r）中寻找target  l>=r 跳出
    while (l < r) {
        int mid = l + (r - l) / 2;
        if (array[mid].compareTo(target) == 0) {
            return mid;
        }
        if (array[mid].compareTo(target) < 0) {
            l = mid + 1;
        }
        if (array[mid].compareTo(target) > 0) {
            r = mid;
        }
    }
    return -1;
}

二分搜索算法实战

实现 leftBound

在算法中，leftBound 是一个基于二分搜索法的变种，其目的是确定在一个有序数组中目标元素的 “最左边界” 位置。这意味着，如果数组中有多个相同的目标元素，leftBound 将返回第一个出现这个元素的索引。如果目标元素不存在于数组中，leftBound 将返回 - 1，以保持数组的有序性。这是一种在有序数据集中快速定位元素的高效方法。

leftBound 的实现需要细微调整普通二分搜索的逻辑。关键点在于如何处理找到目标值的情况：即使找到了目标值，我们也继续搜索其左侧区域，以确保找到的是最左边的匹配项。

以下是使用 Java 语言实现 leftBound 的步骤：

  1. 初始化指针：设定两个指针 low 和 high，分别指向数组的起始位置和末尾位置的下一位。nums [low,high) 左闭右开区间
  2. 开始二分搜索：
  • 计算中间位置 mid。
  • 如果 mid 位置的元素小于目标值，将 low 移至 mid + 1。
  • 如果 mid 位置的元素大于等于目标值，将 high 移至 mid。
  • 检查和返回结果：
  • 搜索结束后，low 将指向目标值的最左边界或者目标值应该插入的位置。
  • 需要检查 low 是否在数组范围内且是否等于目标值，以确认是否找到目标值。

实现方式一 左闭右开区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
     * Java binary search left bound refers to finding the first occurrence of a target value in a sorted array.
     * This can be done using binary search, which has a time complexity of O(log n). Here's an example implementation:
     * 在一个可重复的有序数组中寻找第一次出现的元素
     * 不断向左边逼近
     *
     * @param nums
     * @param target
     * @return
     */
    public static int leftBound(int[] nums, int target) {
        if (nums == null || nums.length == 0) {
            return -1;
        }

        int left = 0;
        int right = nums.length;

        // nums[left,right) 左闭右开区间查询
        while (left < right) {
            int mid = left + (right - left) / 2;

            if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid;
            }

        }

        //  // Check if we found the desired number and 'left' is within bounds. 越界问题分析
        if (left >= nums.length || nums[left] != target) {
            return -1;
        }
        return left;
    }

实现方式二 左闭右闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 实现方式二 左闭右闭区间
private static int findLeftBound(int[] nums, int target) {
    if (nums == null || nums.length == 0) return -1;

    // Perform binary search
    int left = 0;
    int right = nums.length - 1;

    // nums[l,r] 左闭右闭区间
    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] < target)
            left = mid + 1;
        else
            right = mid - 1;
    }

    // Check if we found the desired number and 'left' is within bounds.
    if (left < nums.length && nums[left] == target)
        return left;

    return -1; // Target not found in the array
}

实现 rightBound

rightBound 是二分搜索算法的另一种变体，用于找到目标值在有序数组中的 “最右边界” 位置。如果数组中存在多个相同的目标元素，rightBound 返回最后一个出现这个元素的索引。如果目标元素不存在于数组中，rightBound 会返回 - 1。这是一种在有序数据集中快速定位元素的高效方法。

rightBound 的实现与普通的二分搜索有细微的区别。当找到目标值时，而不是立即返回，算法会继续在右侧区间搜索，以确保找到的是最右边的匹配项。

以下是使用 Java 语言实现 rightBound 的步骤：

  1. 初始化指针：设定两个指针 low 和 high，分别指向数组的起始位置和末尾位置。
  2. 开始二分搜索：
  • 计算中间位置 mid。
  • 如果 mid 位置的元素小于等于目标值，将 low 移至 mid + 1。
  • 如果 mid 位置的元素大于目标值，将 high 移至 mid。
  • 检查和返回结果：
  • 由于循环中 low 可能会超过目标值的最右边界，所以最后需要将 low 减去 1 以指向正确的位置。
  • 检查减去 1 后的 low 是否在数组范围内且是否等于目标值。

实现方式一 左闭右开区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

public static int rightBound(int[] data, int target) {
    if (data == null || data.length == 0) {
        return -1;
    }

    int l = 0;
    int r = data.length;

    // data[l,r)
    while (l < r) {
        int mid = l + (r - l) / 2;
        if (data[mid] == target) {
            l = mid + 1;
        }
        if (data[mid] < target) {
            l = mid + 1;
        }
        if (data[mid] > target) {
            r = mid;
        }
    }

    // l>=r 跳出条件

    if (r - 1 >= 0 && data[r - 1] == target) {
        return r - 1;
    }
    return -1;
}

实现方式二 左闭右闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

private static int findRightBound(int[] nums, int target) {
    if (nums == null || nums.length == 0) return -1;

    // Perform binary search
    int left = 0;
    int right = nums.length - 1;

    // nums[l,r] 左闭右闭区间
    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] > target)
            right = mid - 1;
        else
            left = mid + 1;
    }

    // Check if we found the desired number and 'right' is within bounds.
    if (right >= 0 && nums[right] == target)
        return right;

    return -1; // Target not found in the array
}

插值查找

（Interpolation Search）是一种搜索算法，它是二分搜索的改进。在插值查找中，我们根据要查找的键值对搜索区间进行划分，而不是总是对半分。这种方法对于分布均匀的有序数组是非常高效的。

插值查找原理

插值查找的核心思想是在每次比较时，使用数据分布的信息来预测键值可能存在的位置。它通过一个插值公式来计算可能的位置，而不是总是查找中间位置。如果元素均匀分布，插值查找的平均时间复杂度可以更接近 O (log log n)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public class InsertValueSearch {
    /**
     * 插值查找
     *
     * @param arr    有序数组
     * @param low    搜索的低索引
     * @param high   搜索的高索引
     * @param target 要查找的目标值
     * @return 目标值的索引或-1（如果不存在）
     */
    public static int interpolationSearch(int[] arr, int low, int high, int target) {
        if (low <= high && target >= arr[low] && target <= arr[high]) {
            // 计算插值位置
            int pos = low + ((target - arr[low]) * (high - low)) / (arr[high] - arr[low]);

            if (arr[pos] == target) {
                return pos;
            }

            if (arr[pos] < target) {
                return interpolationSearch(arr, pos + 1, high, target);
            } else {
                return interpolationSearch(arr, low, pos - 1, target);
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        int[] arr = {10, 12, 13, 16, 18, 19, 20, 21, 22, 23, 24, 33, 35, 42, 47};
        int target = 18;
        int index = interpolationSearch(arr, 0, arr.length - 1, target);

        if (index != -1) {
            System.out.println("元素 " + target + " 的索引是: " + index);
        } else {
            System.out.println("元素 " + target + " 在数组中不存在。");
        }
    }
}

这段代码中，interpolationSearch 方法实现了插值查找的逻辑。需要注意的是，由于插值查找依赖于数据的分布，因此它在处理非均匀分布的数据时效率不如二分搜索。

在实际应用中，选择使用插值搜索还是二分搜索取决于数据的特性。

github 项目