《插入排序算法》

发表于 分类于 ， 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟
个人公众号

《算法与数据结构：插入排序算法》

简介

插入排序是一种简单直观的排序算法，它通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实践中对小型数组表现良好，尤其是当数组部分已经排序时。

算法思想

插入排序的基本思想是将待排序的元素看作一个有序表和一个无序表。开始时，有序表中只包含一个元素，而无序表中包含有 n-1 个元素。在排序过程中，每次从无序表中取出第一个元素，将其与有序表中的元素的排序码进行比较，然后将其插入到有序表中的适当位置，形成新的有序表。

关键特点

  • 简单直观：易于理解和实现。
  • 适用于小型数组：对于小数据量效率高。
  • 稳定排序：相等元素的顺序不会改变。

算法原理

  1. 开始排序：从数组的第二个元素开始，这是因为单个元素默认已排序。
  2. 选择元素：选择当前元素，与前面的元素进行比较。
  3. 寻找位置：如果当前元素小于它前面的元素，则将前面的元素向后移动。
  4. 插入元素：重复步骤 3 直到找到当前元素的正确位置，然后将它插入。
  5. 重复过程：对数组中的每个未排序元素重复步骤 2-4。
  6. 完成排序：当所有元素都被考虑过，数组排序完成。

为了更清楚地演示插入排序算法的过程，我们可以使用一个表格来详细展示每一步的操作。假设我们有一个初始数组 [5, 3, 4, 1, 2]，下面是用插入排序对这个数组进行排序的逐步过程：

步骤当前数组状态当前元素已排序部分说明
1[5, 3, 4, 1, 2]3[5]将 3 插入到 5 前面
2[3, 5, 4, 1, 2]4[3, 5]将 4 插入到 5 前面
3[3, 4, 5, 1, 2]1[3, 4, 5]将 1 插入到 3 前面
4[1, 3, 4, 5, 2]2[1, 3, 4, 5]将 2 插入到 3 前面
5[1, 2, 3, 4, 5]-[1, 2, 3, 4, 5]所有元素已排序，算法完成

算法步骤

  • 步骤 1：从数组的第二个元素（3）开始，将其与前面的元素（5）比较，由于 3 小于 5，因此将 3 插入到 5 的前面。
  • 步骤 2：接着处理下一个元素（4），将其与前面已排序部分（3 和 5）进行比较，4 应该插入到 5 前面。
  • 步骤 3：处理元素 1，它比前面的所有元素都小，所以将它移动到数组的最前面。
  • 步骤 4：处理元素 2，它应该被插入到 1 和 3 之间。
  • 步骤 5：此时，所有元素已经排序完成。

每一步中，“当前元素” 是指正在处理的数组元素，“已排序部分” 是指该元素之前的数组部分，它在每一步结束时都已经排好序。

通过这个逐步的表格演示，您可以清楚地看到插入排序算法是如何一步一步地将数组排序的。这种算法特别适合于数组已部分排序的情况，因为这样可以减少比较和移动次数，从而提高效率。

图画演示

创建一个演示数组【3，5，1，2，4】，数组长度为 5，数组表示为 nums [0,5) 左闭右开区间。

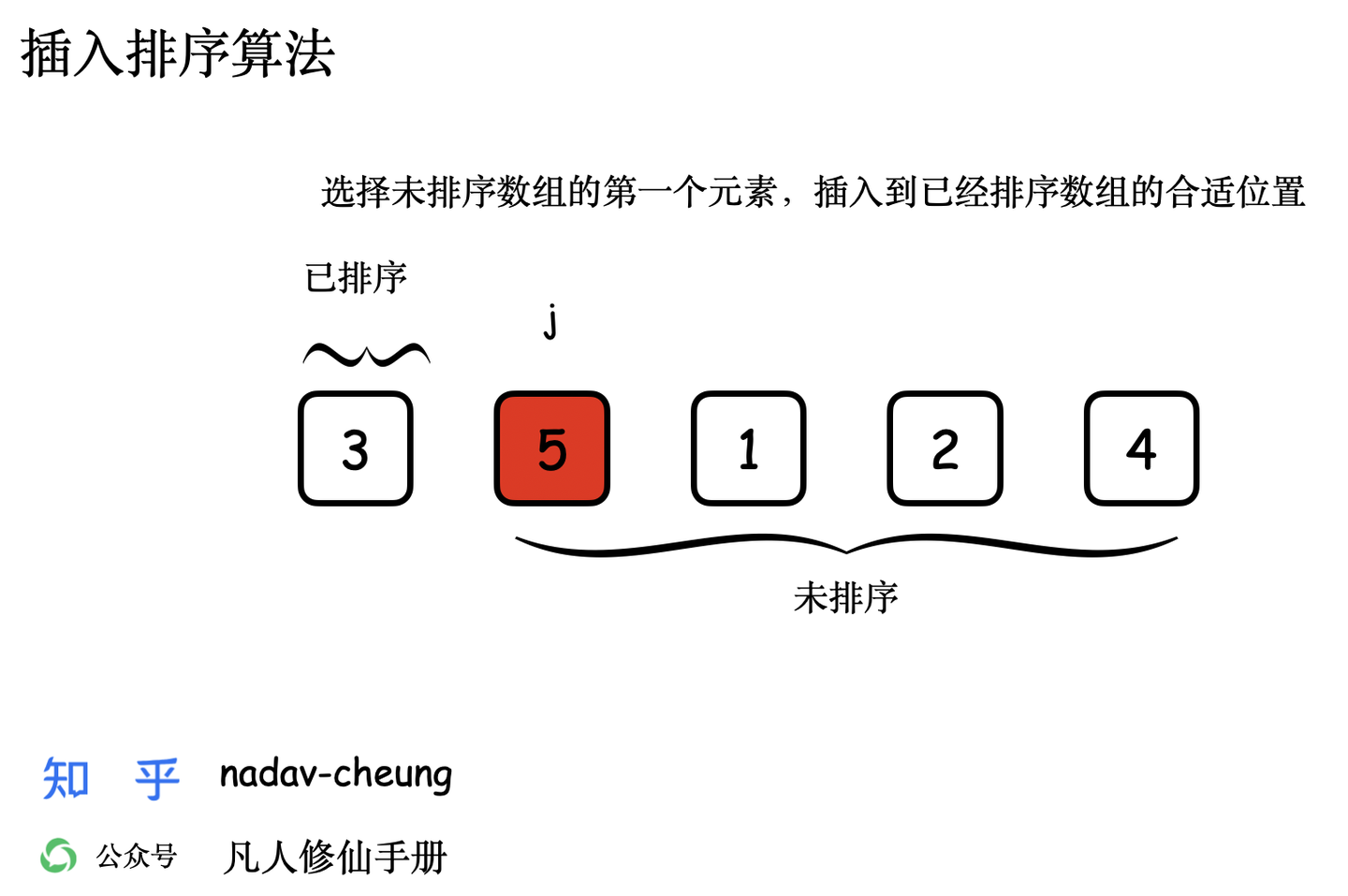
图2 选择元素5，插入已经排序数组中的合适位置

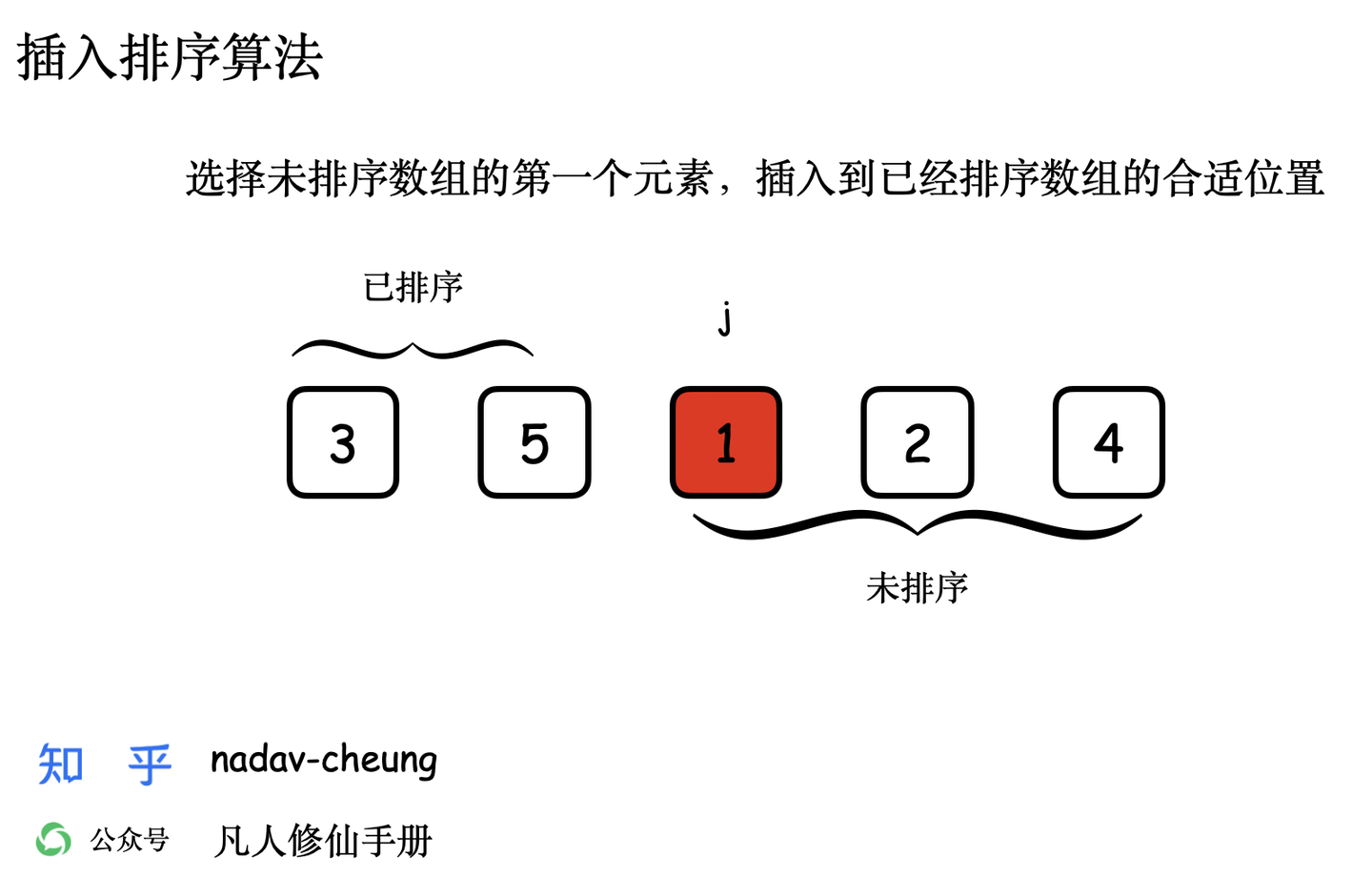
图3 选择元素1，插入已经排序数组中的合适位置

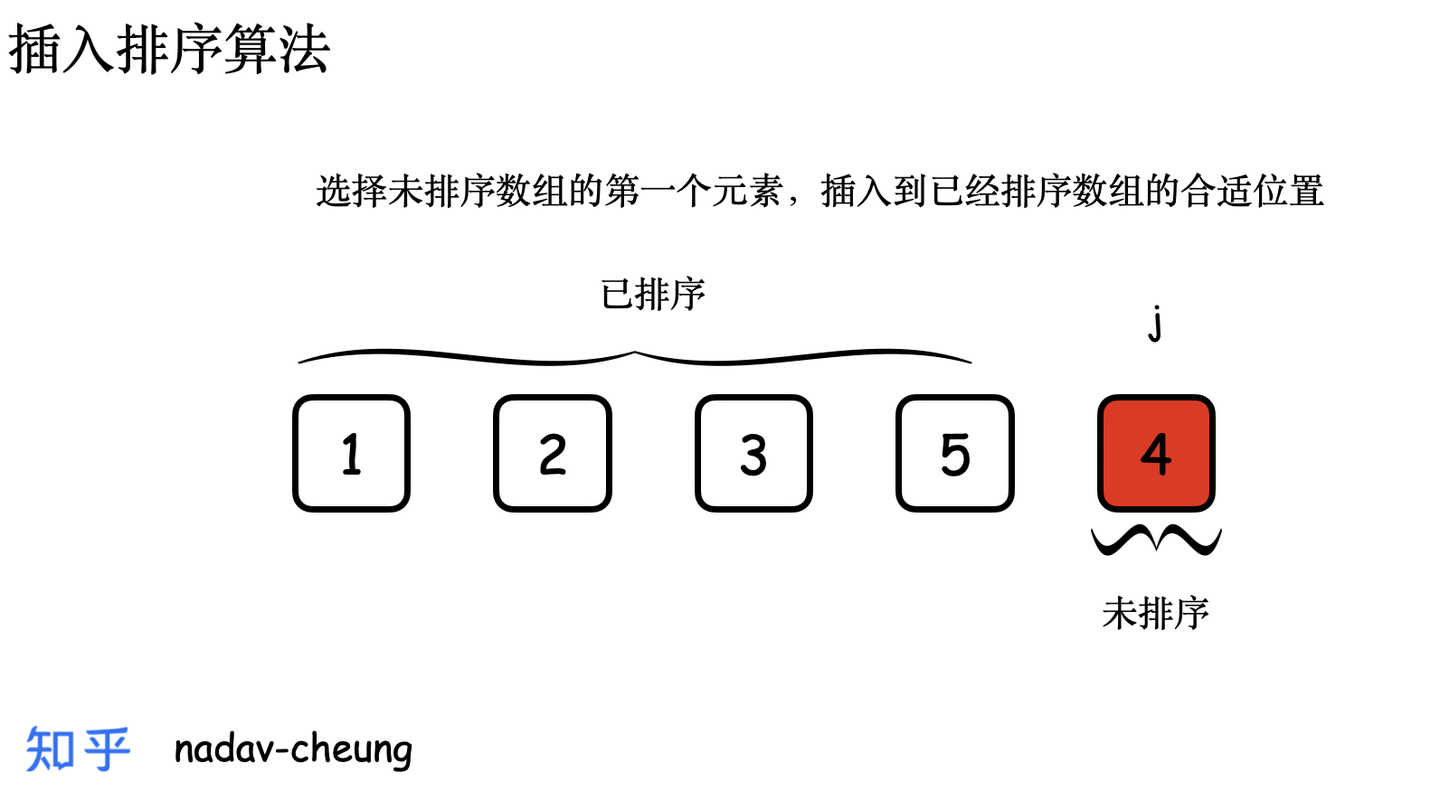
图7 选择元素4，插入已经排序数组中的合适位置

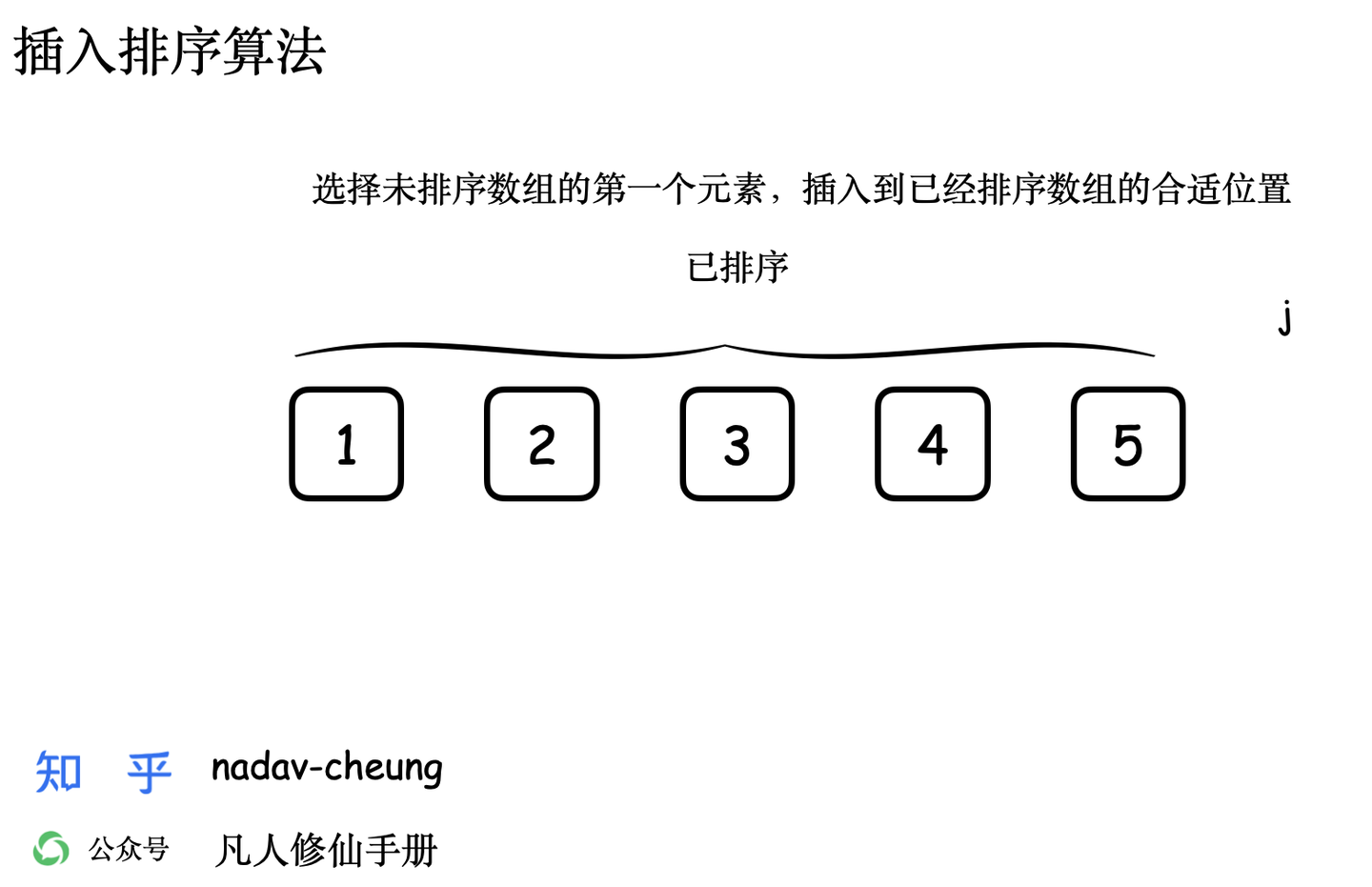
图8 排序完成

动画 GIF 演示

动画GIF演示

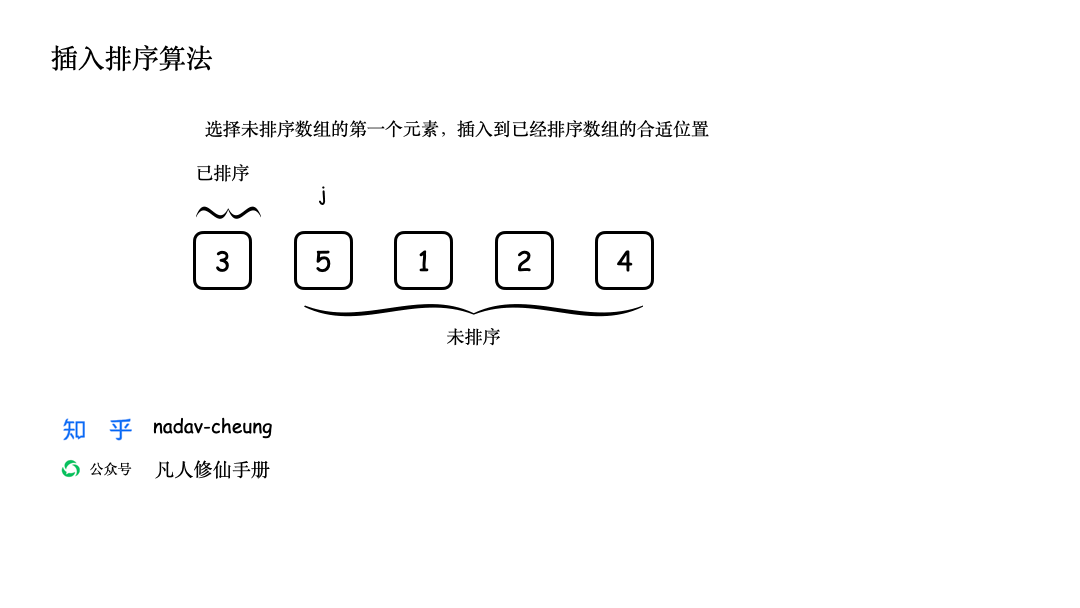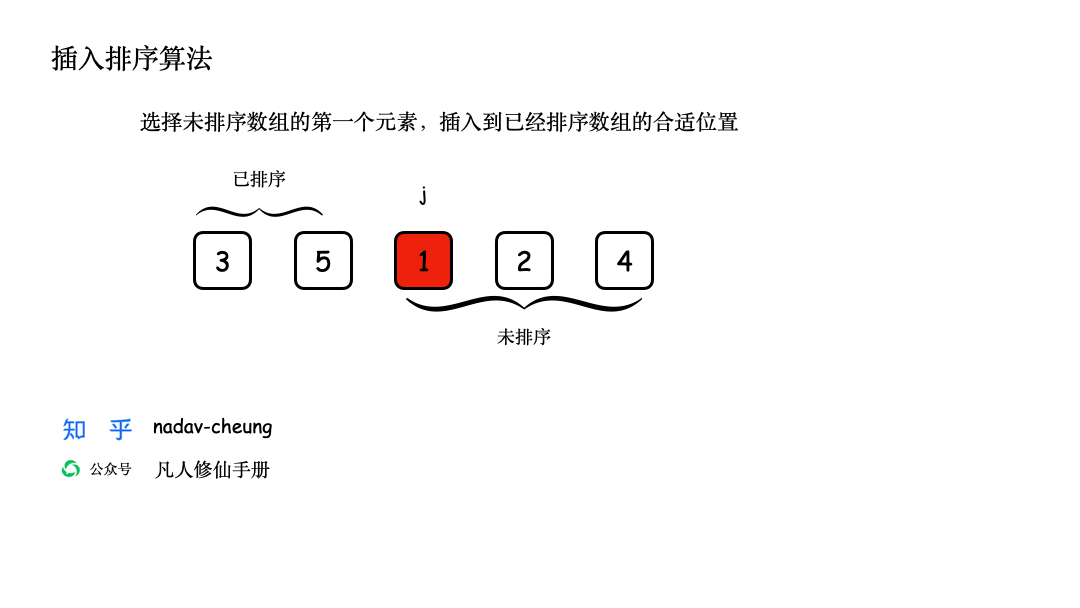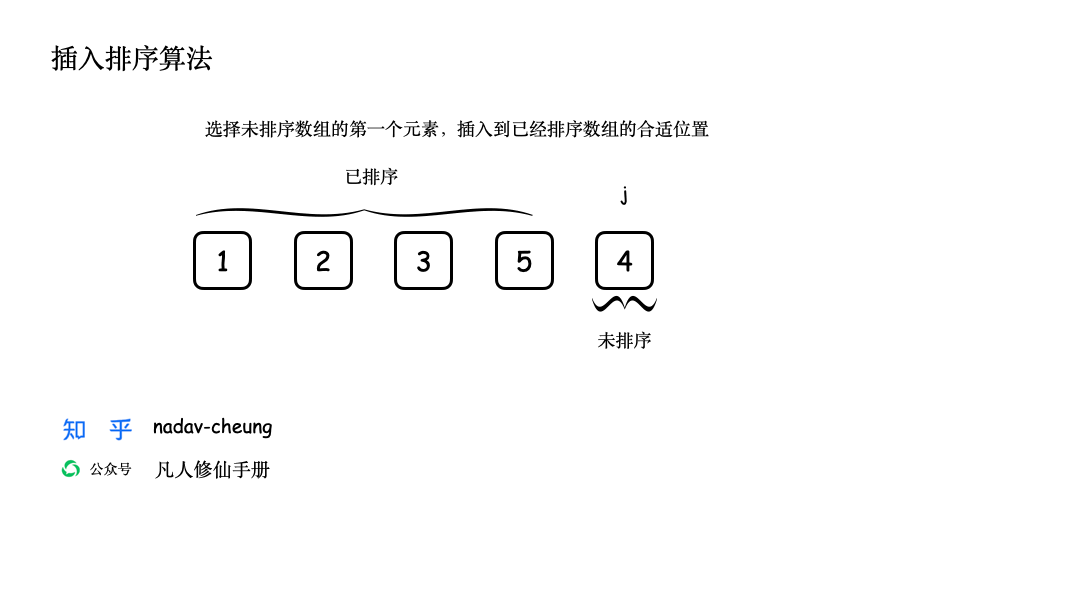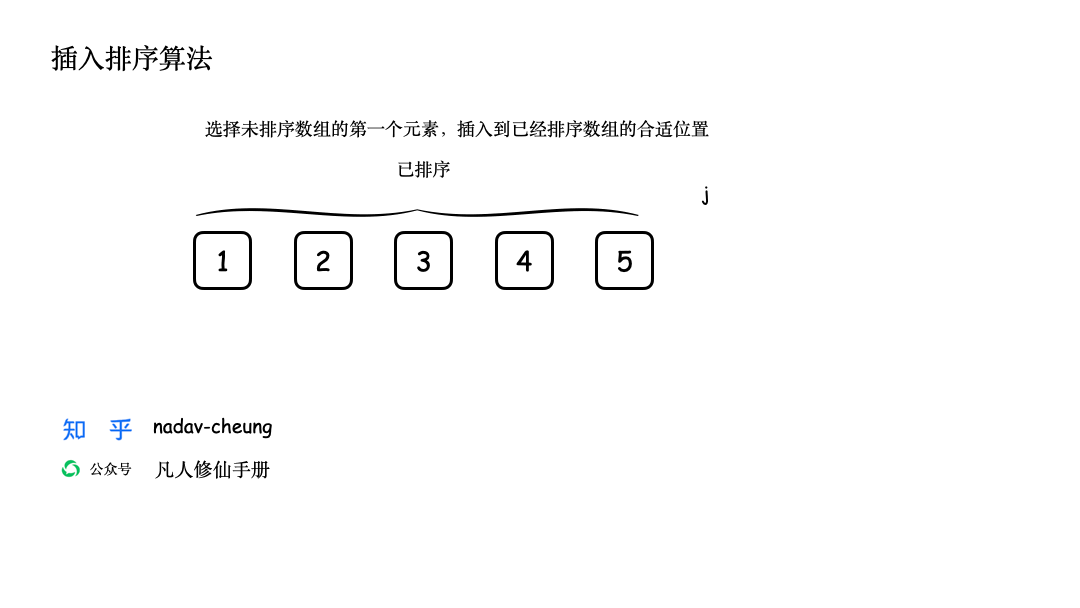
Java 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class InsertionSort {

    private InsertionSort() {
    }

    /**
     * 宏观前提  数组左闭右开
     * i 表示已经排序待数组的长度
     * nums[0,i)已经排序
     * nums[i,n)未排序
     * 每轮排序选择未排序中的第一个元素插入到已经排序的数组的合适位置中，使之成为新的已排序数组
     *
     * @param nums 待排序待数组
     */
    public static void insertionSort(int[] nums) {
        int len = nums.length;
        // 当一个数组中只有一个元素，那么这个数组天然就是已经排序的数组
        // nums[0，1）是已经排序的数组
        for (int i = 1; i < len; i++) {
            // 未排序列表中的第一个元素，待排序元素
            int ret = nums[i];

            // 将待排序元素插入已经排序的数组nums[0,i)中
            // 使数组nums[0,i+1)成为新的已经排序数组
            int j;
            for (j = i; j - 1 >= 0 && ret < nums[j - 1]; j--) {
                nums[j] = nums[j - 1];
            }
            nums[j] = ret;
        }
    }
}

Java 范型接口

1
2
3
4
5
6
7
8
9
10
11
public static <E extends Comparable<? super E>> void insertionSort(E[] nums) {
    for (int i = 1; i < nums.length; i++) {
        // 待排序代元素
        E ret = nums[i];
        int j;
        for (j = i; j - 1 >= 0 && ret.compareTo(nums[j - 1]) < 0; j--) {
            nums[j] = nums[j - 1];
        }
        nums[j] = ret;
    }
}

github 项目