Tree的基本概念

《算法与数据结构:Tree的基本概念》

树的基本概念

树（Tree）结构简介

树是一种层级数据结构，非常适合用来表示具有层级关系或者需要快速搜索操作的数据集合。它由节点Nodes组成，这些节点通过边Edges相连。一个树结构有以下特点：

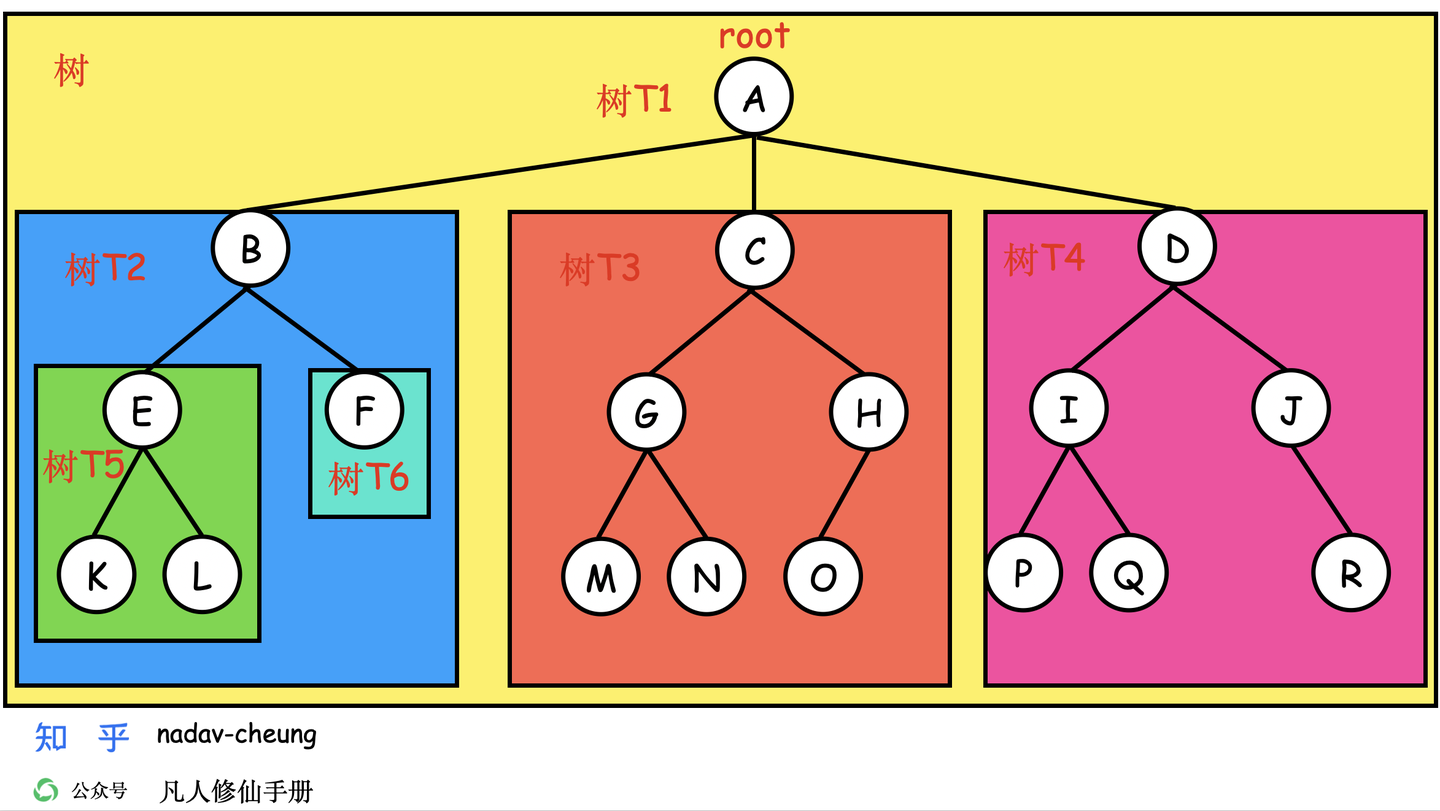
• **树与子树：**树是一个有限集合，子树则是该集合的子集。就像套娃一样，一棵树下面还包含着其子树。比如，树T1的子树为 树T2、T3、T4，树T2的子树为 T5、T6。 上图中还有许多子树没有标记出来 。
• **结点(Node)：**一个结点包括一个数据元素和若干指向其子树分支。比如，在树T1 中，结点A 包括一个数据元素A 和 三个指向其子树的分支。上图中共有 18 个结点 。
• **根结点(Root)：**一颗树只有一个树根，这是常识。在数据结构中,“树根”即根节点。比如，结点A 是树 T1的根结点; 结点C是树T1的子结点，是树 T3 的根结点。
• **度(Degree)：**一个结点拥有的子树数。比如，结点A的度为 3，结点G的度为 2，结点H 的度为 1。
• **叶子(Leaf)/ 终端结点：**度为 0 的结点被称为叶子结点，很形象。比如对于树 T1来说，结点F、K、L、M、N、O、P、Q、R 均为叶子节点。
• **分支结点 / 非终端结点：**和叶子结点相对，即度不为 0 的结点。
• **内部结点：**顾名思义在树内部的结点，即不是根结点和叶子结点的结点。
• **双亲节点或父节点：**若一个节点含有子节点，则这个节点称为其子节点的父节点。如上图，A是B的父节点。
• **孩子节点或子节点：**一个节点含有的子树的根节点称为该节点的子节点。 如上图，B是A的孩子节点。
• **兄弟节点：**具有相同父节点的节点互称为兄弟节点。 如上图，B、C是兄弟节点。
• **堂兄弟节点：**双亲在同一层的节点互为堂兄弟节点。如上图，E、F、G、H互为堂兄弟节点。
• **节点的祖先：**从根到该节点所经分支上的所有节点。如上图，A是所有节点的祖先。
• **子孙：**以某节点为根的子树中任一节点都称为该节点的子孙。如上图，所有节点都是A的子孙。
• **层次(Level)：**从根结点开始，根为第一层，根的孩子为第二层，依次往下。比如，结点K在树 T1中的层次为 4。
• **深度(Depth)/ 高度：**指树的最大层次。比如，树 T1的高度为 4 。
• 有序树: 树中任意节点的子结点之间有顺序关系，这种树称为有序树 。
• 无序树 : 树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树 。
• **森林：**由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除，则该树就变成了一片森林，森林中的树由原来根节点的各棵子树构成。

树的类型

• 二叉树（Binary Tree）：每个节点最多有两个子节点。
• 二叉搜索树（Binary Search Tree, BST）：左子节点总是小于或等于父节点，右子节点总是大于或等于父节点。
• 平衡二叉树（AVL Tree）：任何两个子树的高度差不超过一。
• 红黑树（Red-Black Tree）：一种自平衡二叉搜索树。
• B树和B+树：常用于数据库和文件系统。

二叉树

二叉树的基本结构

1
2
3
4
5
6
7
8
9

class Node<E> {
    E key;
    Node<E> left, right;
    
    public Node(E item) {
        key = item;
        left = right = null;
    }
}

二叉树的定义

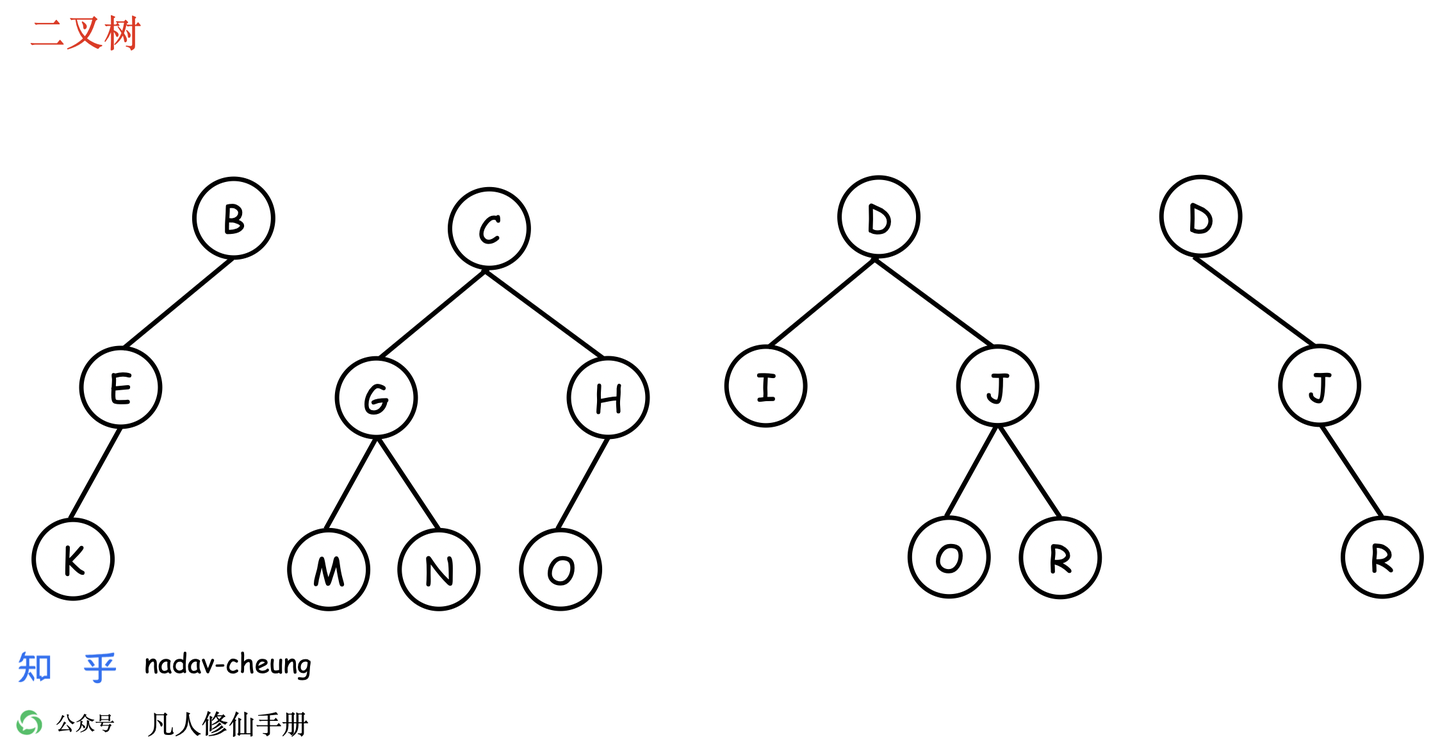
1. 二叉树的前提是一棵树，满足上述对树的定义。
2. 二叉树节点最多有两个子节点，分别是左子节点和右子节点

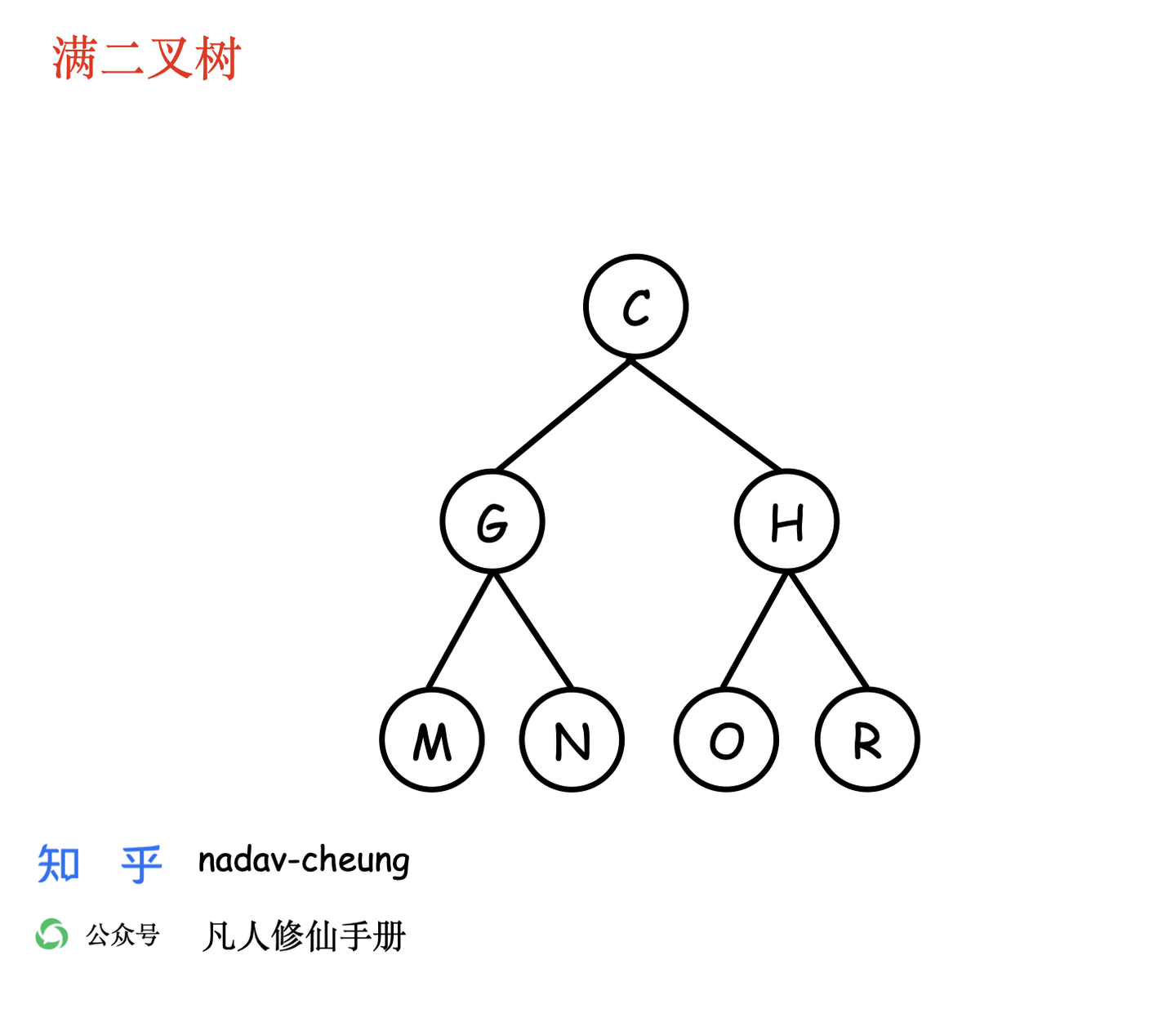
满二叉树

1. 如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

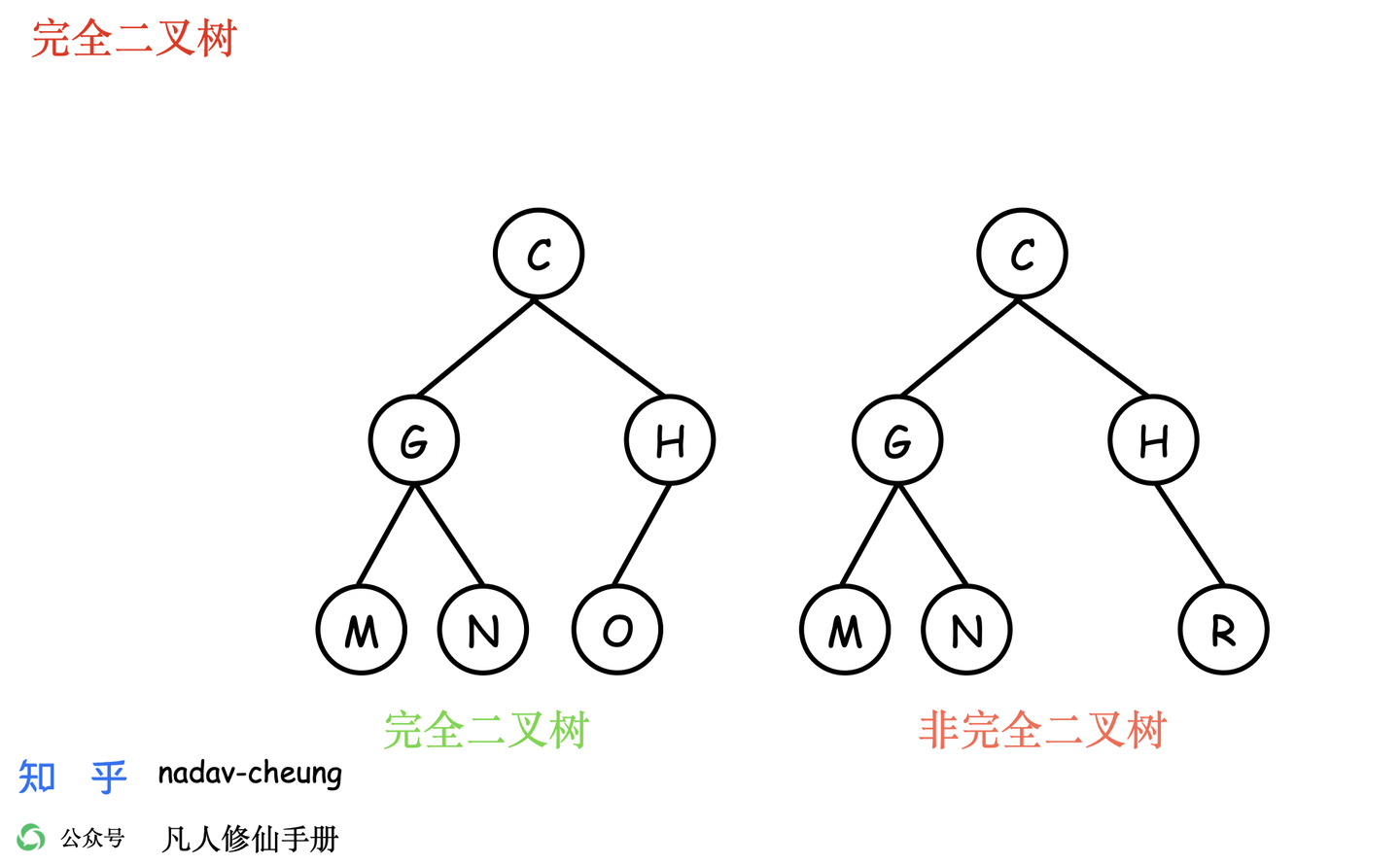
完全二叉树

1. 如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

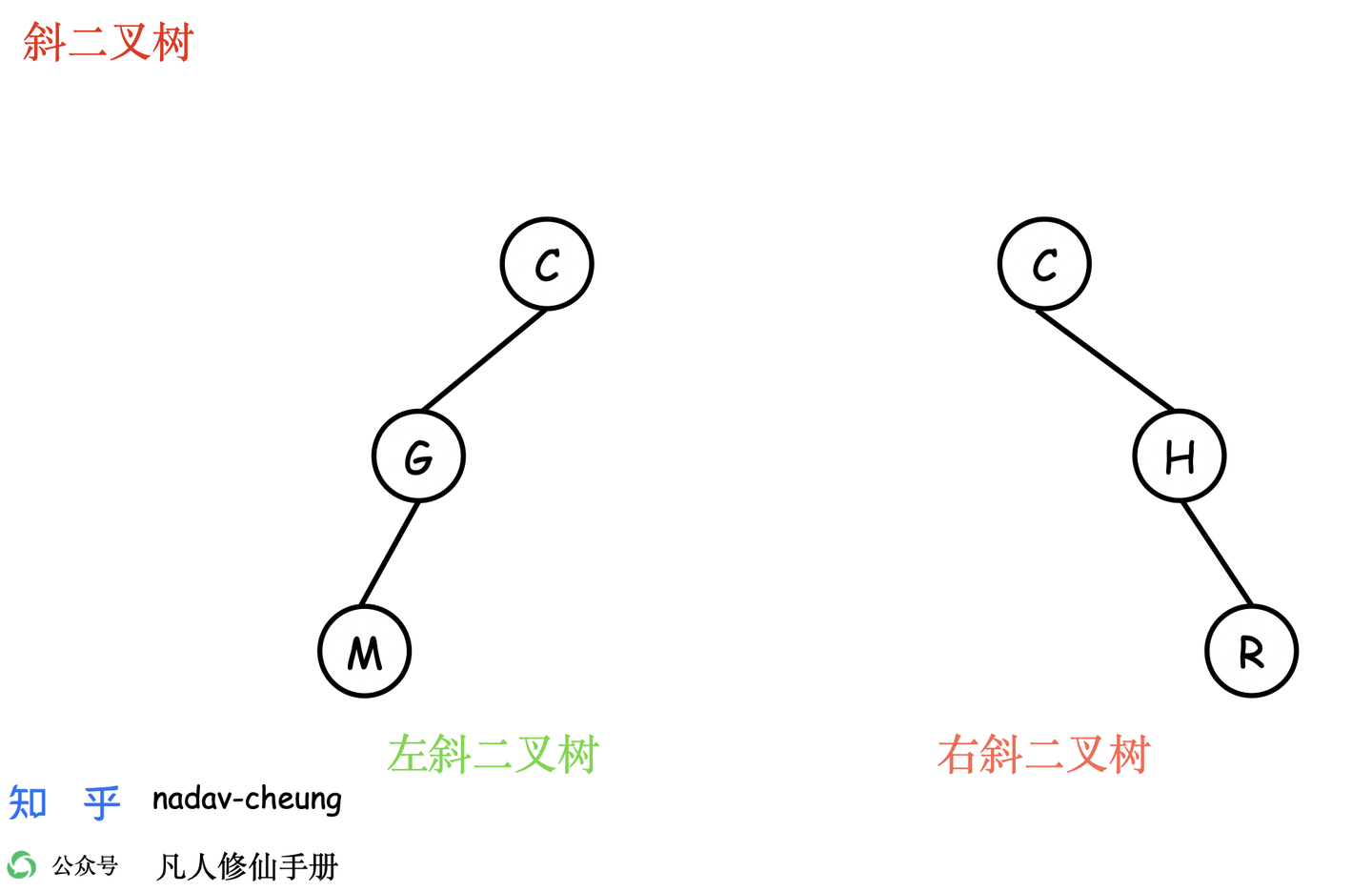
斜二叉树

1. 这个很好理解，斜二叉树就是斜的二叉树，所有的节点只有左子树的称为左斜树，所有节点只有右子树的二叉树称为右斜树。

二叉树的存储

1. 二叉树多采用两种方法进行存储，基于数组的顺序存储法和基于指针的二叉链式存储。

基于数组的顺序存储

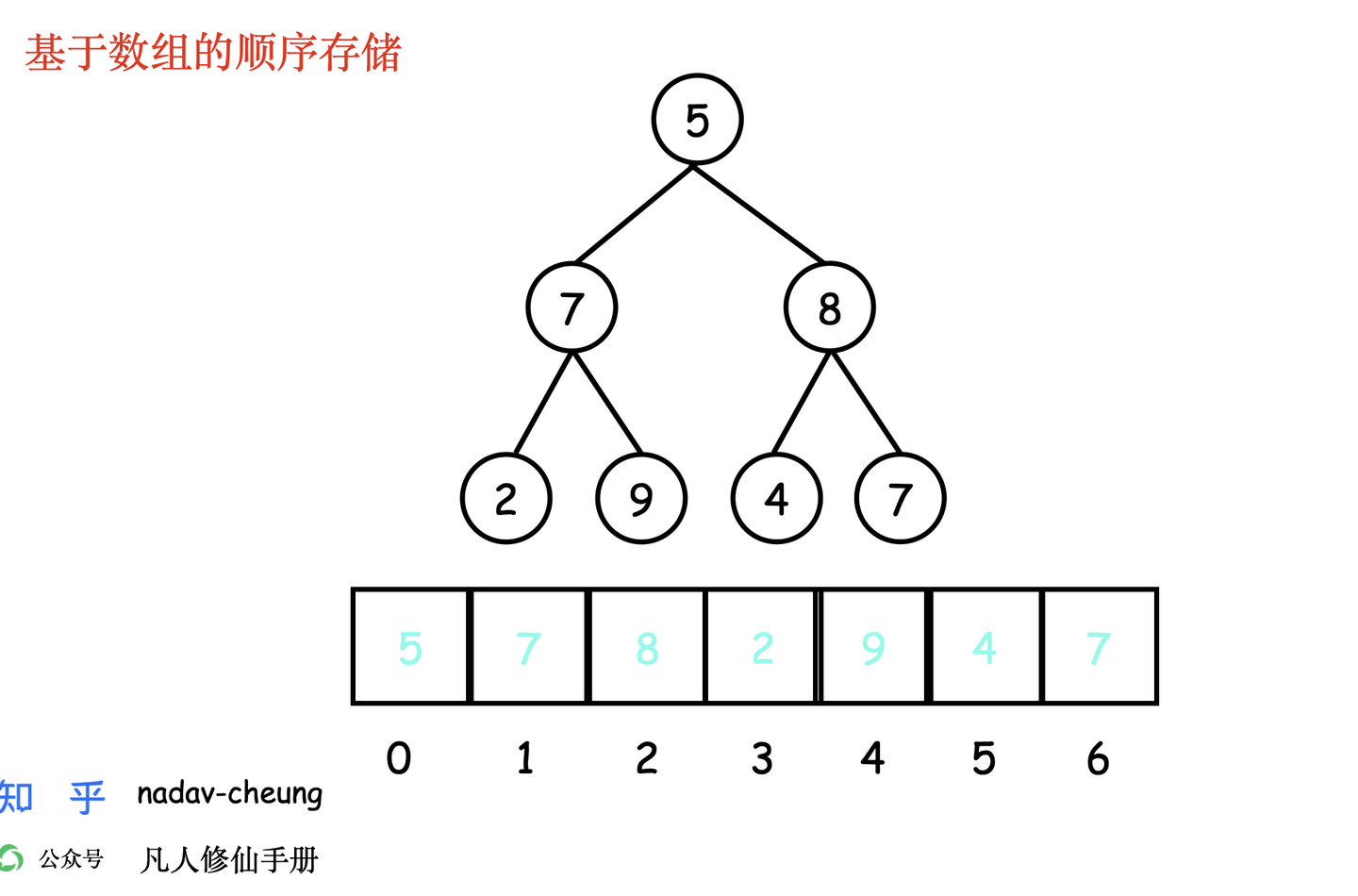
左孩子节点:
$$
leftchild = parent\ast2+1
$$
右孩子节点:
$$
rightchild = parent\ast2+2
$$
父亲节点:
$$
parent = （child -1）\div 2
$$

基于指针的链表存储

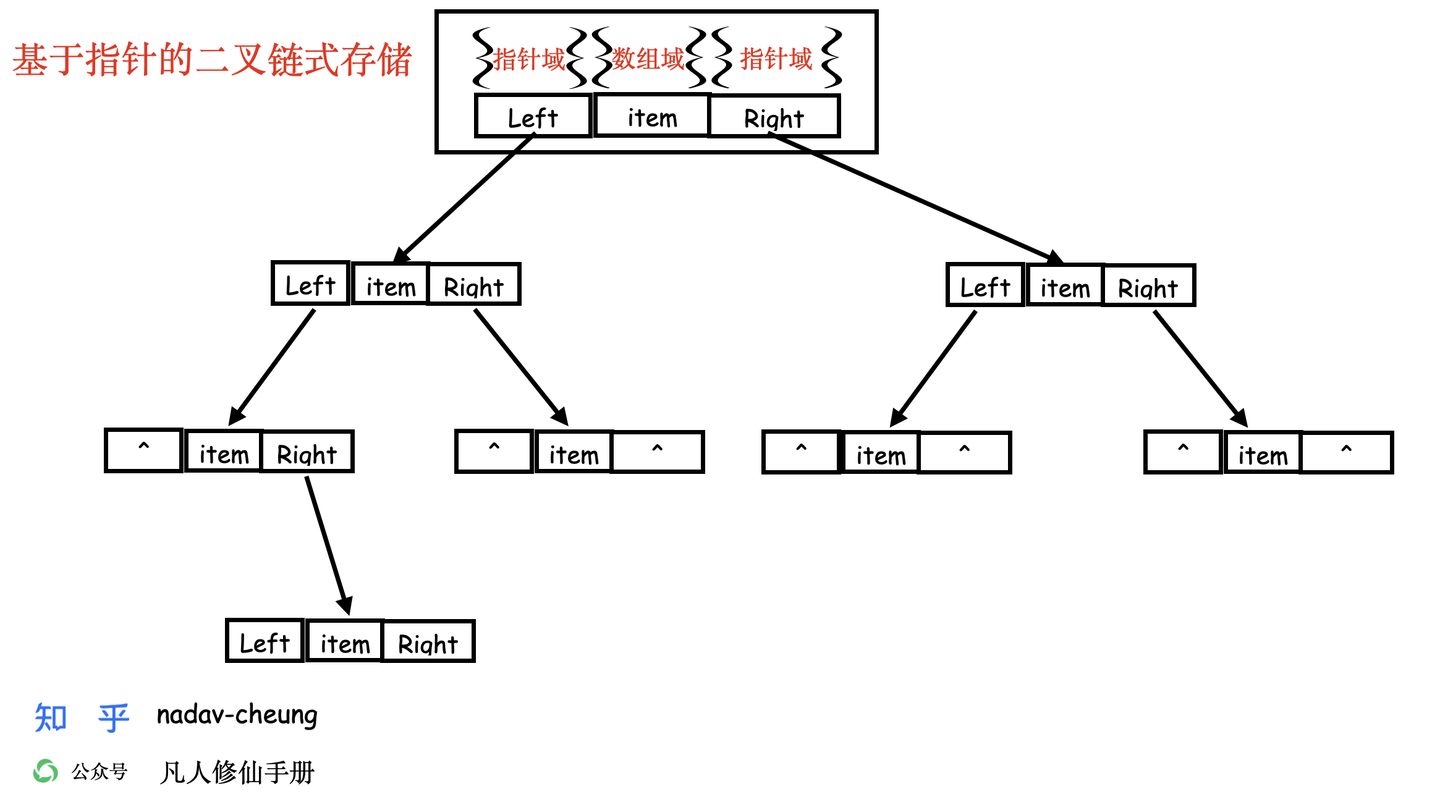
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

static class Node<K, V> {
    public K key;
    public V value;
    public Node<K, V> left, right;

    public Node(K key, V value, Node<K, V> left, Node<K, V> right) {
        this.key = key;
        this.value = value;
        this.left = left;
        this.right = right;
    }

    public Node(K key, V value) {
        this(key, value, null, null);
    }
}

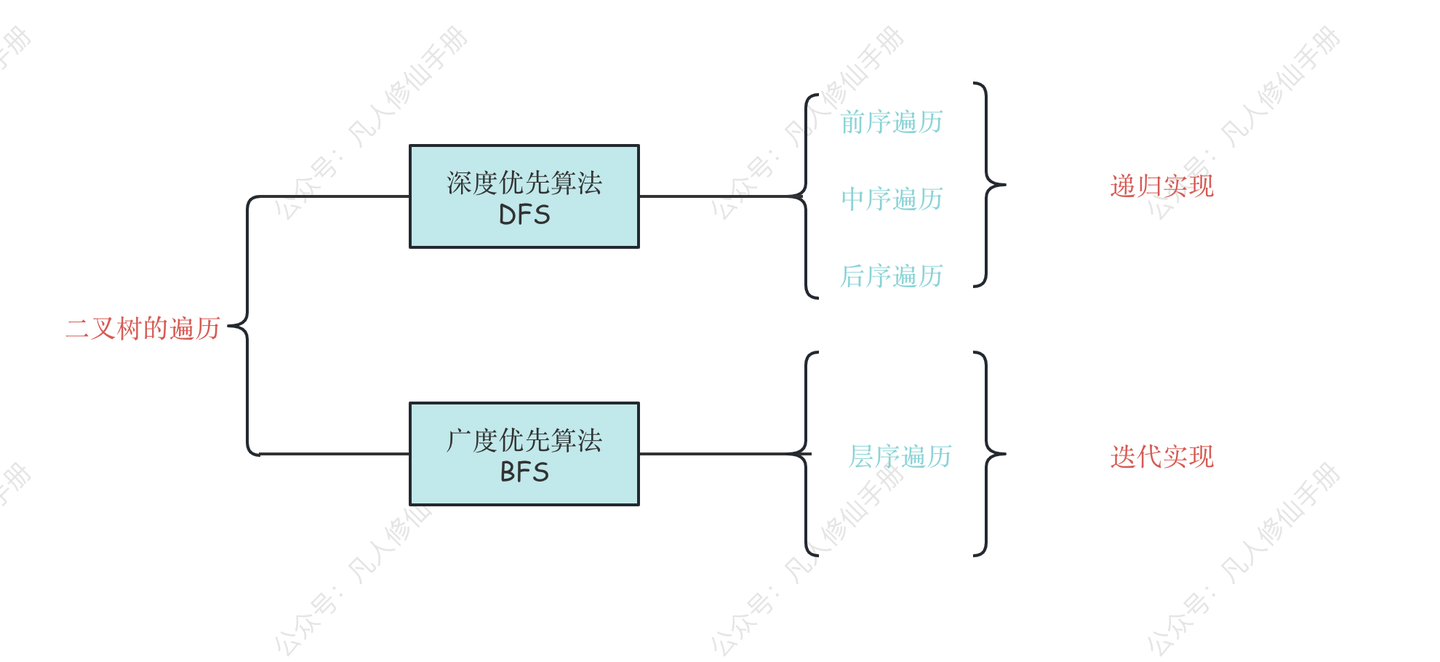
二叉树的遍历

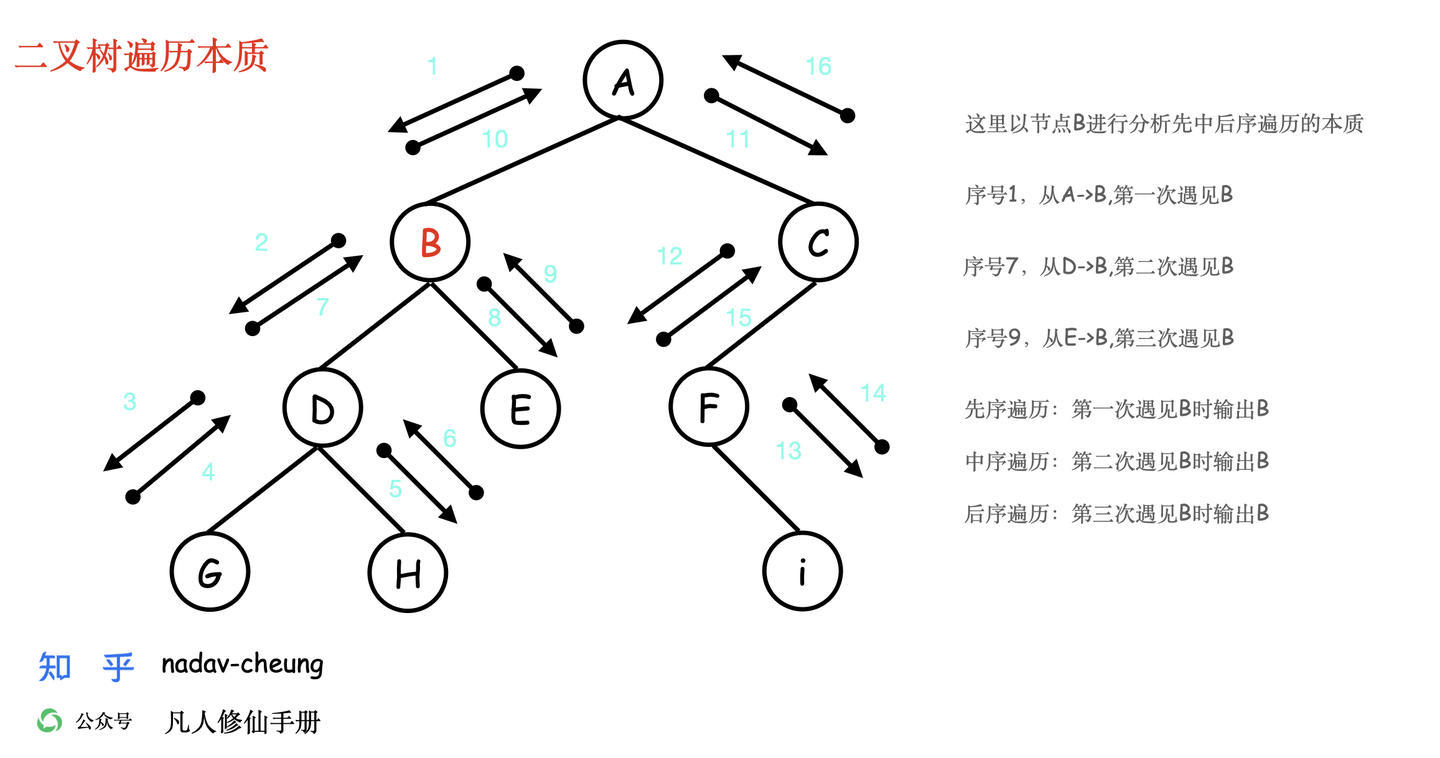
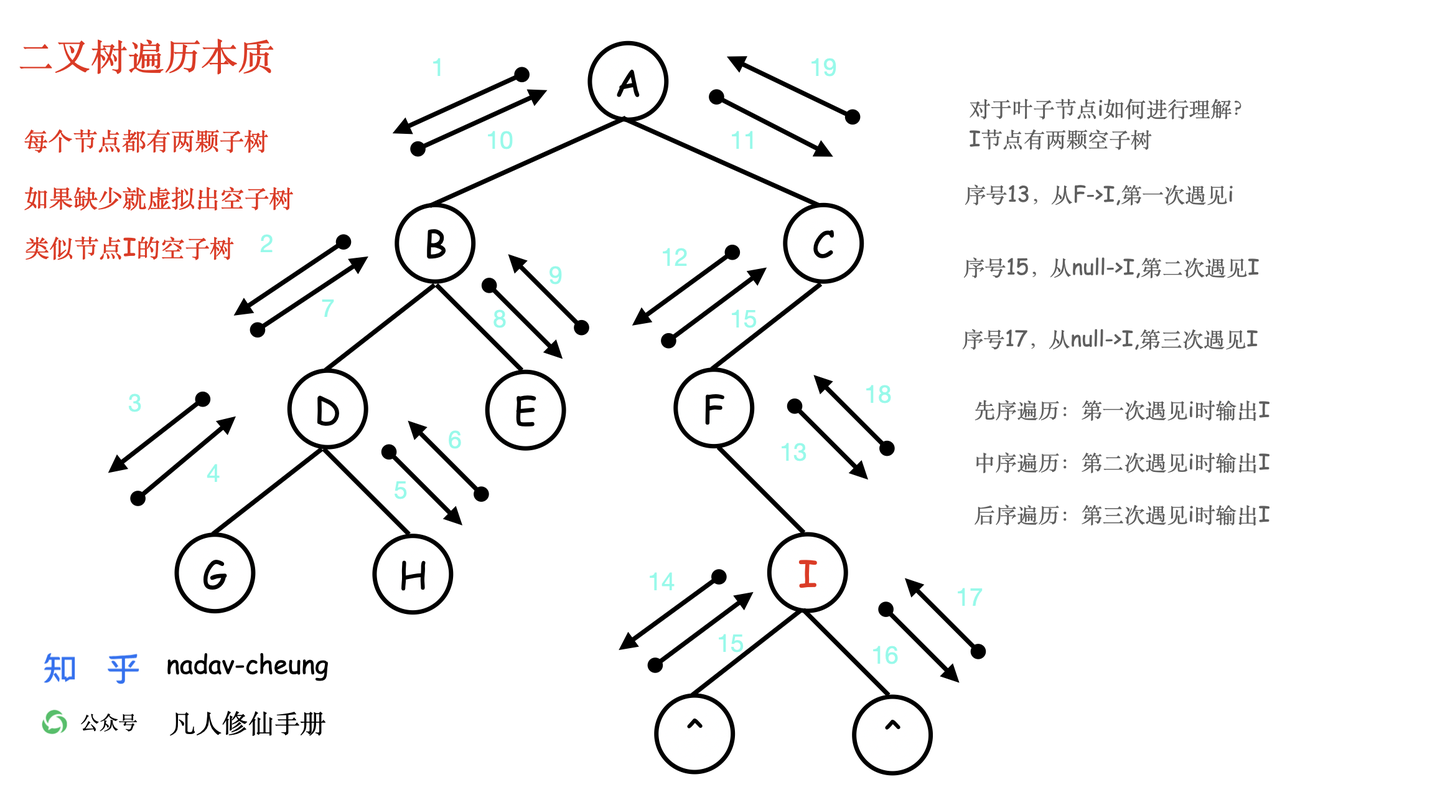
前序遍历

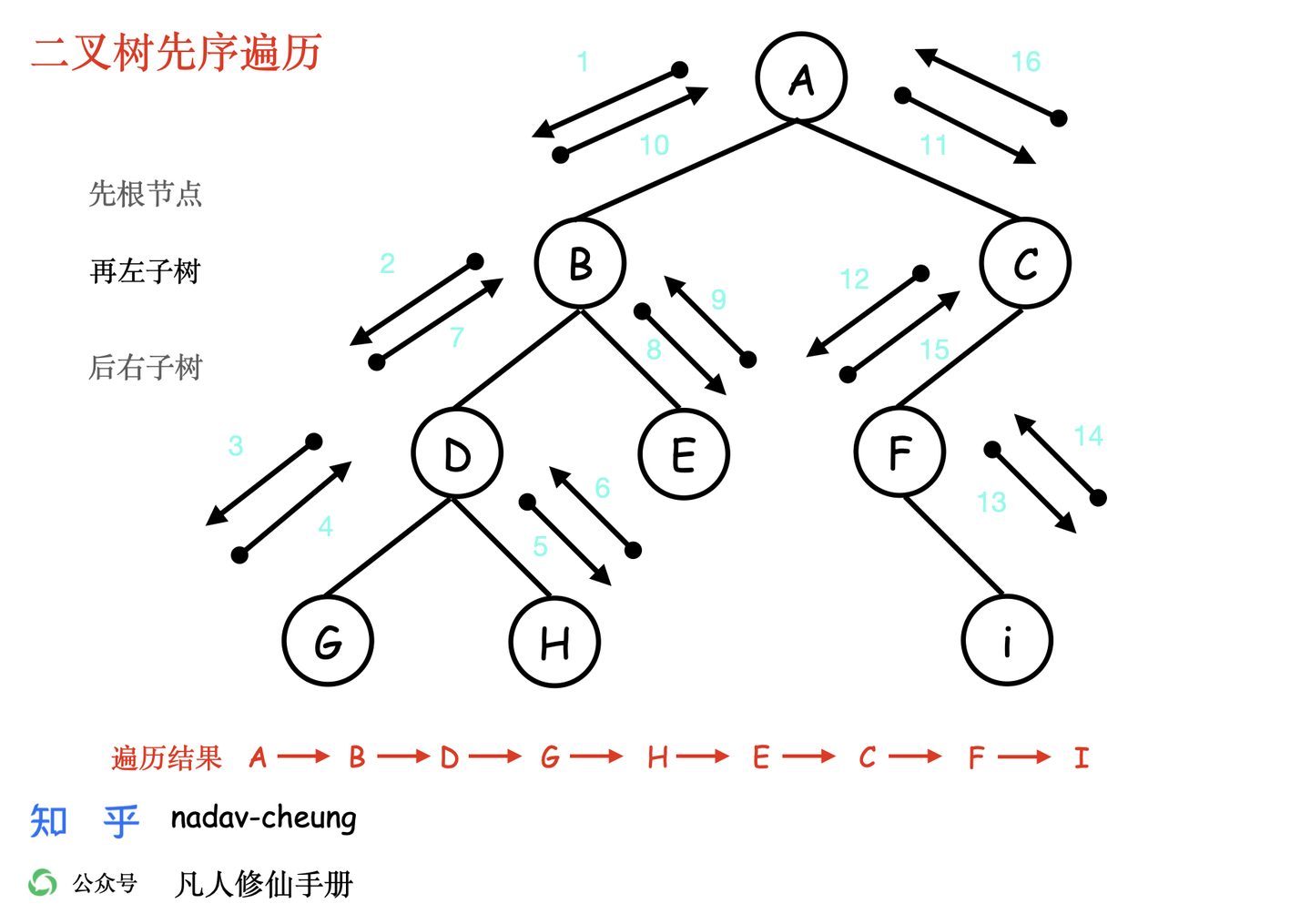
1. 前序遍历的顺序是, 对于树中的某节点,先遍历该节点,然后再遍历其左子树,最后遍历其右子树。

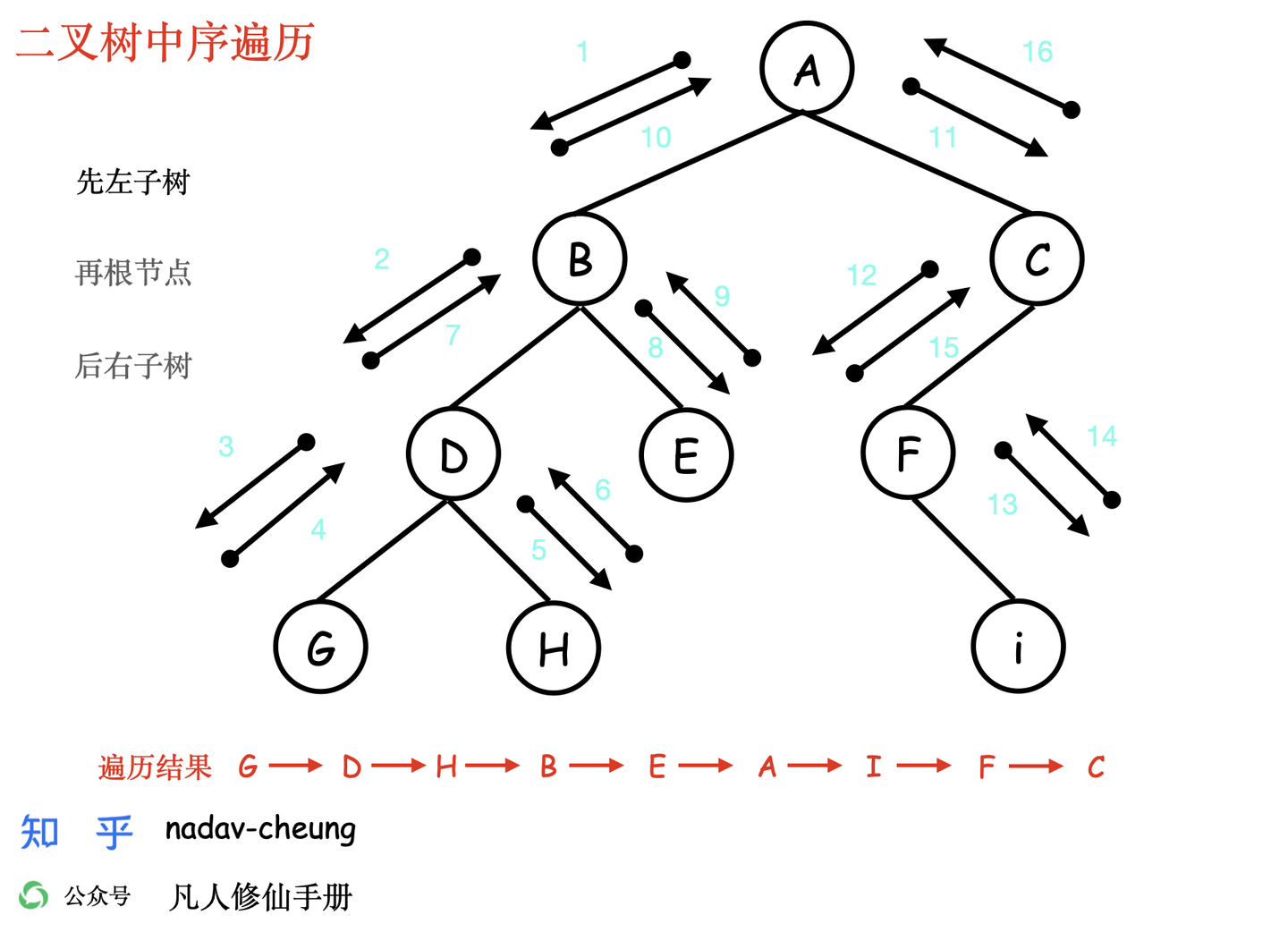
中序遍历

1. 中序遍历的顺序是, 对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树。

后序遍历

1. 后序遍历的顺序是,对于树中的某节点, 先遍历该节点的左子树, 再遍历其右子树, 最后遍历该节点。

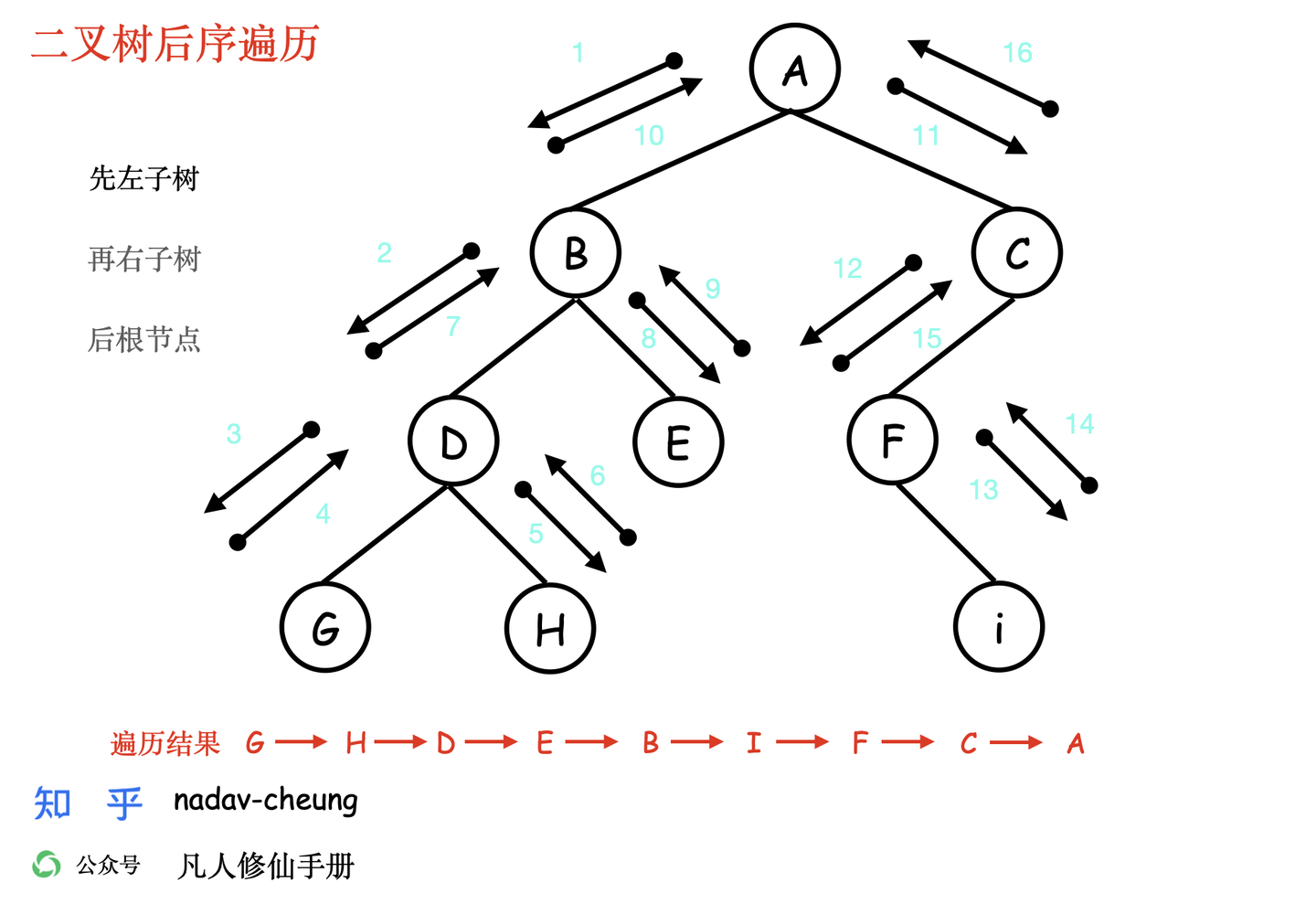
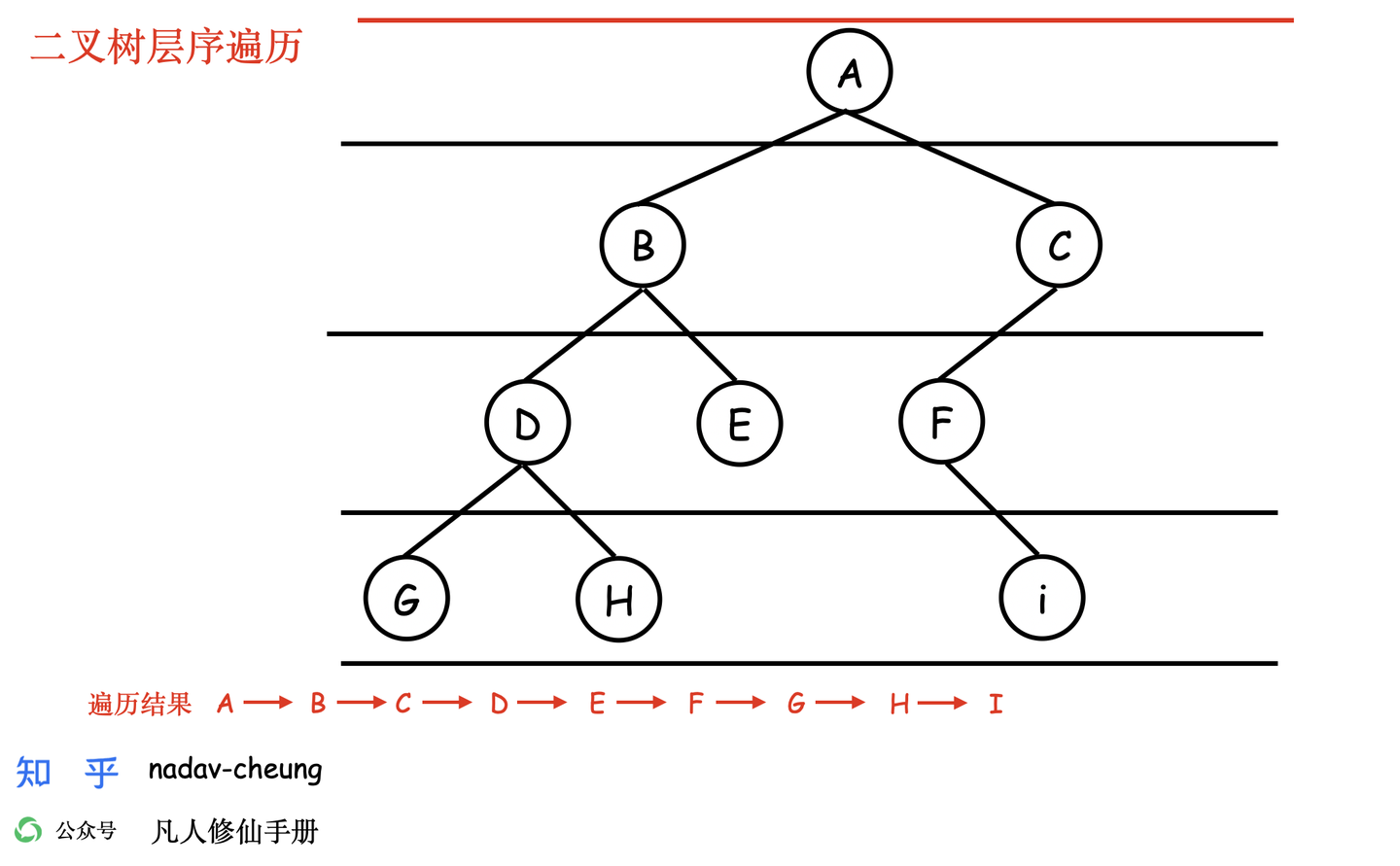
层序遍历

1. 顾名思义,一层一层的遍历。

遍历衍生算法

1. 归并排序 后续遍历
2. 快速排序 前序遍历

github项目