《HeapSort》

发表于 分类于 ， 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟
个人公众号

《算法与数据结构：HeapSort》

简介

堆排序是一种高效的排序算法，它利用了堆的数据结构特性来排序元素。在堆排序中，首先将待排序的序列构造成一个堆，然后将堆顶的最大（或最小）元素与堆尾元素交换，然后调整堆结构，继续选择堆顶的元素，直到序列排序完成。

堆的类型和性质

  • 最大堆：父节点的值总是大于或等于子节点的值。在数组中，对于每个元素 i，其子节点位于 2 * i + 1 和 2 * i + 2。
  • 最小堆：父节点的值总是小于或等于子节点的值。同样地，子节点的位置与最大堆相同。
  • 性质：堆总是一棵完全二叉树。这意味着除了最底层，每层都是完全填满的，而最底层则尽可能地从左到右填满。

堆的实现

堆前置知识

在 Java 中，可以使用数组来实现堆。数组中的每个位置对应堆中的一个节点，父节点和子节点的位置关系可以通过数组索引轻松找到。这种数据结构使得堆操作的时间复杂度保持在对数级别。

img

堆排序算法步骤

  1. 构建堆：将给定数组构建成最大堆（或最小堆）。
  2. 排序：将堆顶元素（最大或最小）与堆的最后一个元素交换，然后减小堆的大小并重新调整堆，重复这个过程直至堆为空。
  3. 构建堆的过程：将一个无序数组转换成一个堆。这通常通过 “堆化” 过程实现，即从最后一个非叶子节点开始向上调整，确保每个子树都遵循堆的性质。
  4. 堆排序的过程：移除堆顶元素（最大或最小），将其放置在数组的末尾，然后重新调整剩余元素以维持堆的性质。重复这一过程直到所有元素都被排序。

堆排序示例

对整数数组进行堆排序

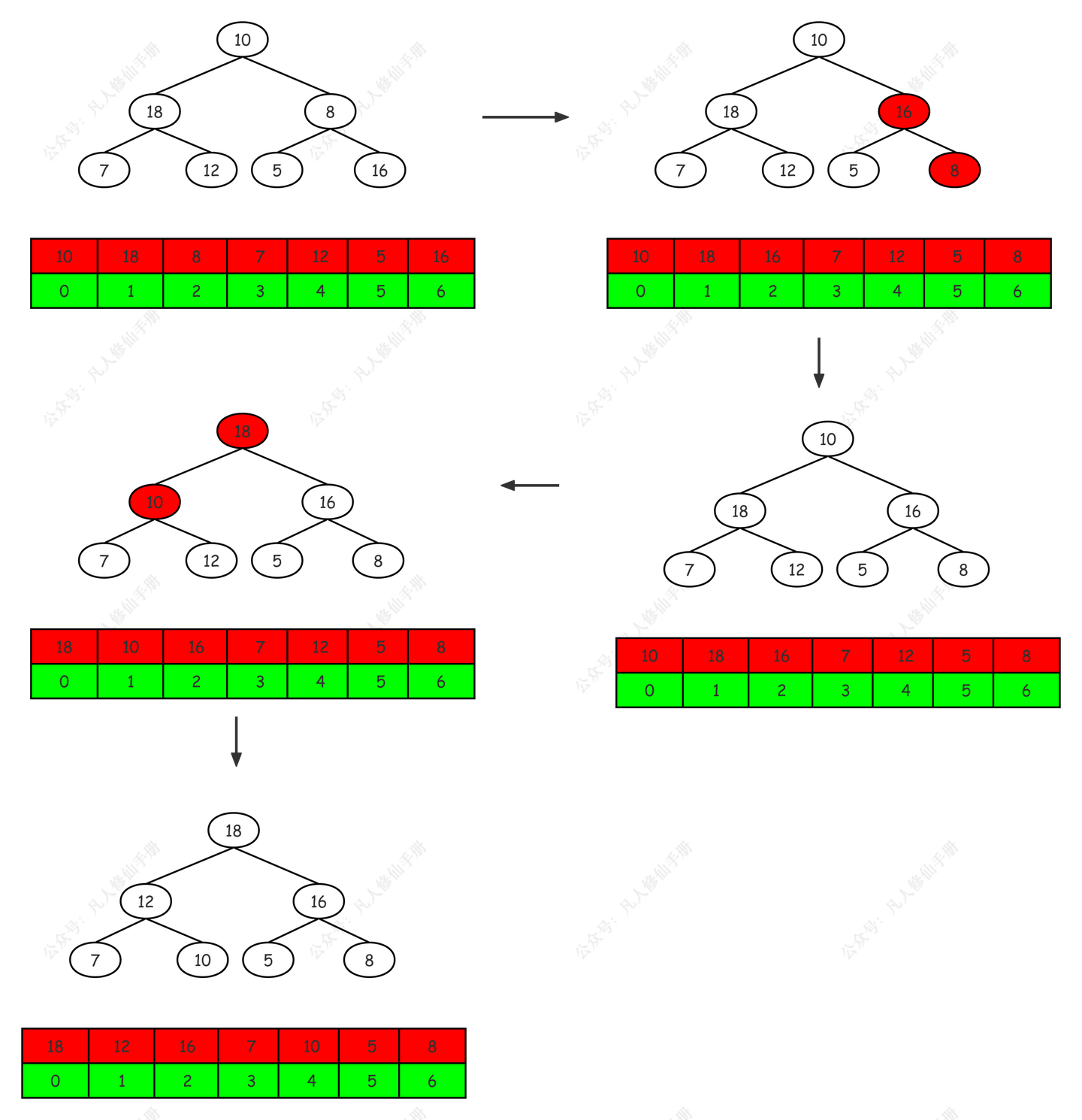
考虑数组 [10, 18, 8, 7, 12, 5, 16]，我们希望通过堆排序对其进行排序。

构建最大堆：

  • 开始时，数组表示为 [10, 18, 8, 7, 12, 5, 16]。
  • 对数组进行堆化，构建最大堆。
  • 经过调整，得到最大堆：[18, 12, 16, 7, 10, 5, 8]。

img

排序过程：

  • 完成堆排序的数组是：[18, 12, 16, 7, 10, 5, 8]。
  • 将堆顶元素（18）与最后一个元素（8）交换：[8, 12, 16, 7, 10, 5, 18]。
  • 将除去最后一个元素（已排序部分）的剩余部分调整为最大堆：[16, 12, 8 7, 10, 5] | [18]。
  • 再次将堆顶元素（16）与最后一个元素（5）交换：[6, 12, 8 7, 10, 16] | [18]。
  • 将除去最后一个元素（已排序部分）的剩余部分调整为最大堆：[12, 10 8, 7, 5] | [16, 18]
  • 继续这个过程，直到所有元素都被排序：最终数组为 [5, 7, 8, 10, 12, 16, 18]。

img

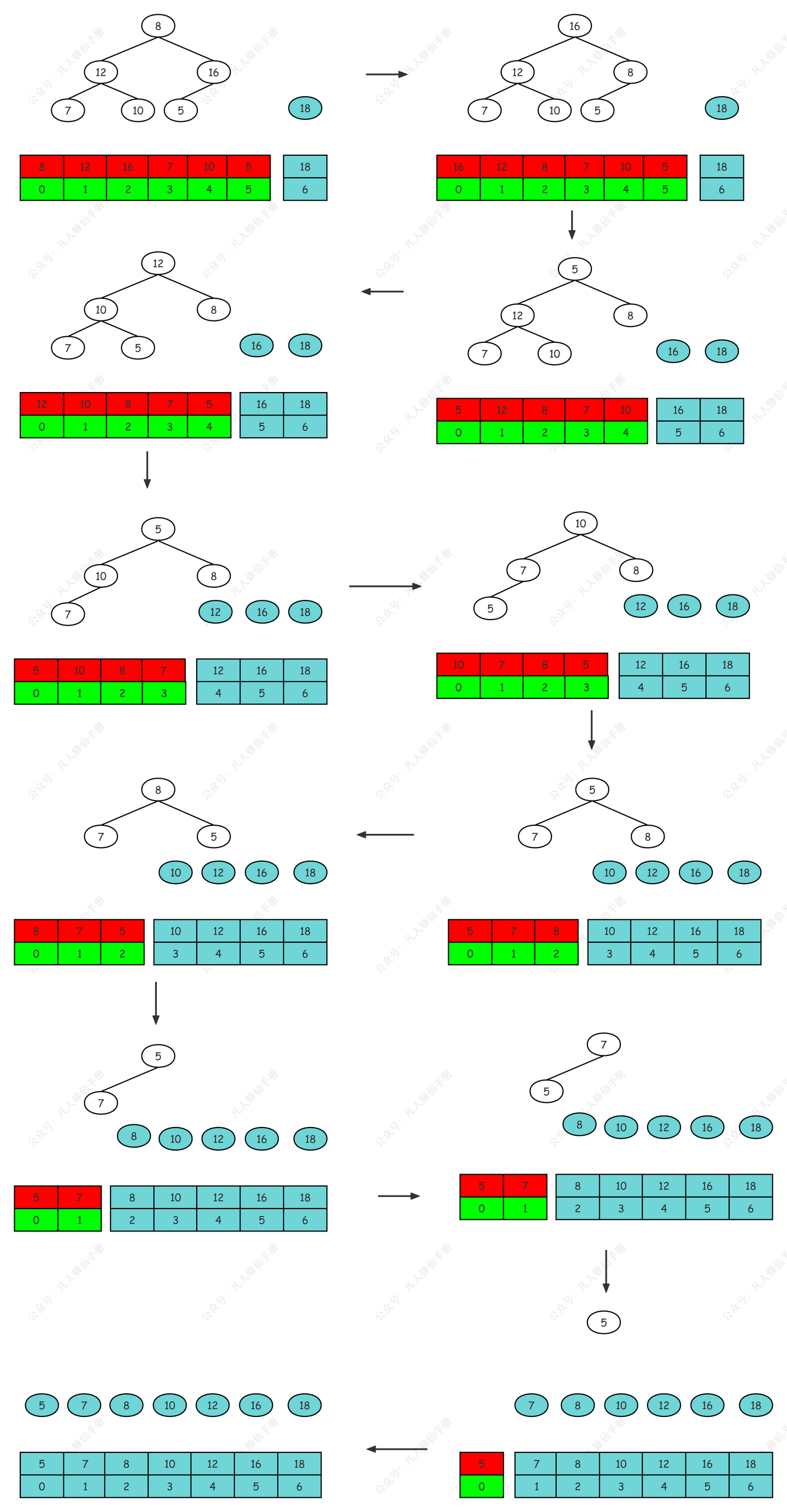
在这个过程中，每次都将最大元素移至数组的末尾，并在剩余的数组部分重建最大堆，直到所有元素都被排序。

代码示例

建堆 heapify

1
2
3
4
5
private void heapify(T[] nums, int length) {
    int i = (length >>> 1) - 1;
    for (; i >= 0; i--)
        siftDownComparable(i, nums[i], nums, length);
}

下沉 siftDown

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 在位置 k 处插入项 x，通过将 x 沿着树重复降级直到它小于或等于其子项或者是叶子来保持堆不变性。
 */
private void siftDownComparable(int k, T x, T[] nums, int length) {
    int half = length >>> 1;           // loop while a non-leaf

    // 将 x 沿着树重复降级直到它大于或等于其子项或者是叶子来保持堆不变性。
    while (k < half) {
        // 记录两个孩子节点中的较大节点
        int child = leftChild(k); // assume left child is least

        // 记录 两个孩子节点中的较大者
        T c = nums[child];

        // 右边孩子节点
        int right = child + 1;

        // 右边孩子节点存在 并且 左边孩子节点大于右边孩子节点 寻找两个孩子节点中的较小者
        if (right < length && c.compareTo(nums[right]) < 0)
            // 更新孩子节点和索引
            c = nums[child = right];

        // 满足堆的性质
        if (x.compareTo(c) > 0)
            break;

        // 不满足性质 在k的位置插入较大的孩子节点c
        nums[k] = c;

        // x 沿着树降级 将k更新为较大的孩子节点 尝试在k处重新插入x
        k = child;
    }
    // 跳出循环 在位置 k 处插入项 x，
    nums[k] = x;
}

堆排序 Sort

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void sort(T[] nums) {
    int length = nums.length;

    // 构建最大堆
    heapify(nums, length);

    // 逐个从堆顶取出元素到数组末尾，完成排序
    for (int i = length - 1; i > 0; i--) {
        // 队尾元素
        T heapTail = nums[i];

        // 取出堆顶元素 放入堆尾
        T heapHead = nums[0];
        nums[i] = heapHead;

        // 在堆顶插入队尾元素 这时候会违反堆的元素 执行siftDown
        siftDownComparable(0, heapTail, nums, i);
    }
}

总结

  • 时间复杂度：平均和最坏情况下都是 O (nlogn)。
  • 空间复杂度：O (1)，因为它是就地排序。
  • 不稳定性：堆排序是一种不稳定的排序算法，因为在堆顶的元素与子树的最后一个元素交换时，可能会改变相等元素的初始顺序。

理解堆排序主要就是理解堆的特性和 siftDown 操作原理

github 项目