《Heap》

《算法与数据结构:Heap》
堆
堆是一种数据结构,它是一种完全二叉树,具有以下特点:
- 堆是完全二叉树,即每个节点都有两个子节点。
- 堆是一种有序树,即对于任意节点 n,如果 n 有左子节点 l 和右子节点 r,则 n 的值比 l 和 r 的值都大或都小。
- 堆可以分为最大堆和最小堆两种,最大堆的根节点是堆中最大的元素,最小堆的根节点是堆中最小的元素。
堆的特性
堆是一种特殊的树形数据结构。它满足两个主要特性:
- 结构性:堆是一棵完全二叉树,这意味着除了最后一层外,每一层都是完全填满的,而且最后一层的所有节点都尽可能地集中在左侧。
- 堆属性:在最大堆中,任何一个父节点的值都大于或等于它的子节点;在最小堆中,则相反,父节点的值小于或等于其子节点。
- 存储:堆可以用数组来存储。对于数组中的任意元素,其子节点和父节点的位置可以通过简单的数学运算得到。
- 类型:堆主要有两种类型 —— 最大堆和最小堆。
- 最大堆:每个父节点的值都大于或等于其子节点的值。
- 最小堆:每个父节点的值都小于或等于其子节点的值。
堆(Heap)数据结构
堆的应用
堆主要用于实现优先队列,并广泛用于各类算法中,如堆排序、图算法中的 Dijkstra 最短路径算法等。
堆的操作
堆的主要操作有插入、删除和堆排序。堆的插入和删除操作的时间复杂度均为 O (logn),其中 n 为堆中节点的数量。堆排序是将一个无序的数组转换成一个有序的数组合并进行排序的过程,时间复杂度为 O (nlogn)。
堆的数组实现
在数组实现中,我们使用如下方法计算父节点和左右孩子节点之间的关系。
对于数组中任何位置 i 的元素:
它的父节点位置是 :
$$
parent=(i-1)\div2,i>0
$$
它的左子节点位置是:
$$
leftchild=i\times2+1
$$
它的右子节点位置是:
$$
rightchild=(i+1)\times2
$$
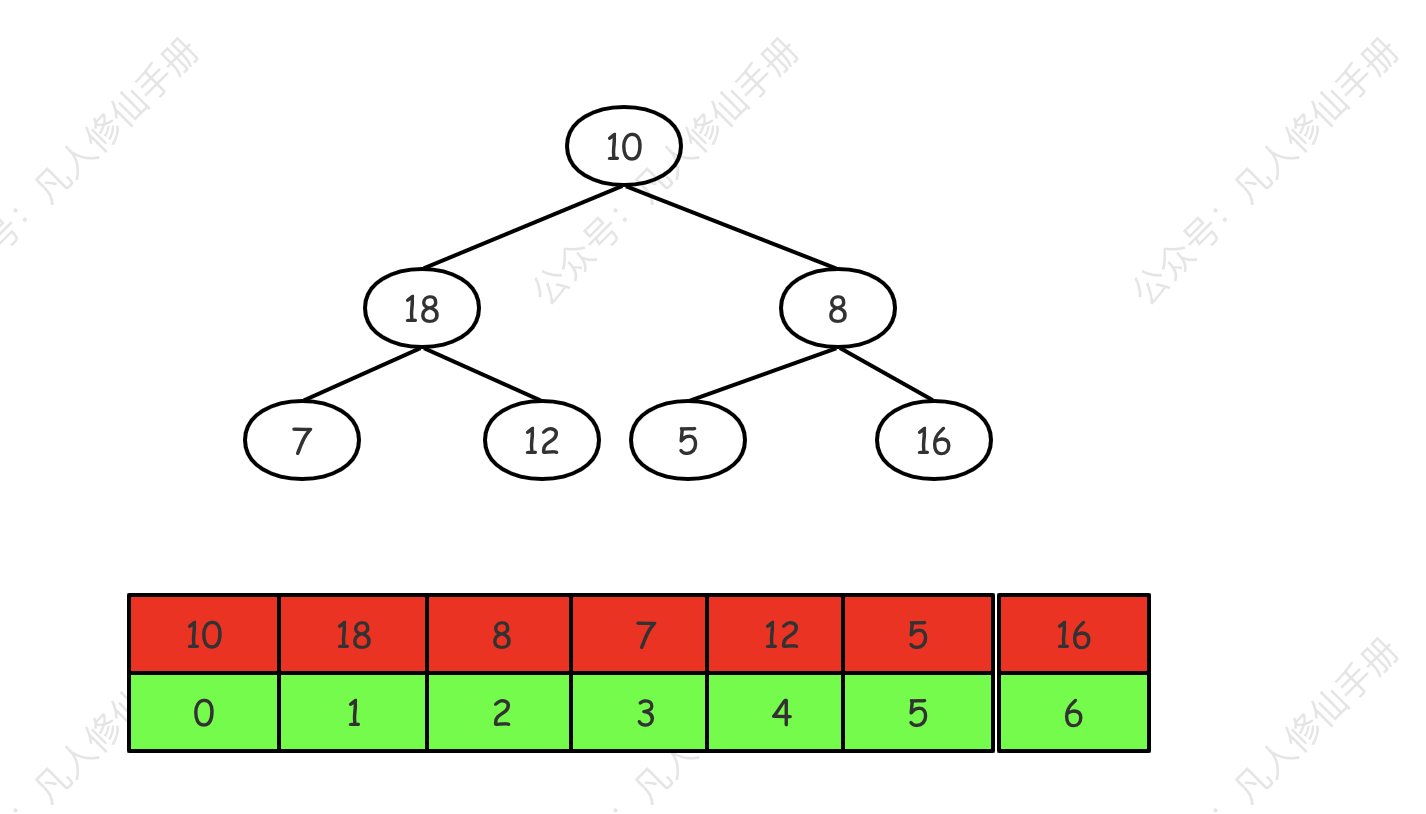
从数据存储结构上来看,最大堆 / 最小堆是一个数组。
从数据逻辑结构来看,最大堆 / 堆小堆事一颗完全二叉树。
siftUp 和 siftDown 是在堆数据结构中用于维护堆属性的两个重要操作。这两个操作确保在插入新元素或移除堆顶元素后,堆仍然保持其结构和性质。我们来具体探讨一下这两个操作的原理。
siftUp 原理
siftUp(也称为上浮、上滤或泡上来)主要用于插入操作。当一个新元素被添加到堆的末端时,它可能会违反堆的性质。siftUp 的目的是重新调整元素的位置,以恢复堆的性质。
1、过程:
- 将新元素添加到堆的末尾(即数组的最后一个位置)。
- 比较新元素与其父节点的值(在最小堆中,父节点的值应小于子节点)。
- 如果新元素的值小于其父节点的值,则交换这两个节点。
- 继续向上比较和交换,直到新元素的父节点的值小于或等于新元素,或者新元素已经到达堆顶(成为根节点)。
2、目的:
- 确保在将新元素添加到堆后,堆仍然保持最小堆(或最大堆,取决于堆的类型)的性质。
siftUp 源码
1 | /** |
siftUp 具体实现1
2
3
4
5
6
7
8
9
10
11
12
13
private static <T> void siftUpComparable(int k, T x, Object[] es) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
int parent = parent(k);
Object e = es[parent];
if (key.compareTo((T) e) >= 0)
break;
es[k] = e;
k = parent;
}
es[k] = key;
}
过程
将新元素添加到堆的末尾(即完全二叉树的最后一个节点)。
比较这个新元素与其父节点的值。
- 在最大堆中,如果新元素大于其父节点,它们就交换位置。
- 在最小堆中,如果新元素小于其父节点,它们同样交换位置。
重复步骤 2,直到新元素到达堆顶,或者找到了合适的位置(即满足堆的性质)。
siftUp 演示
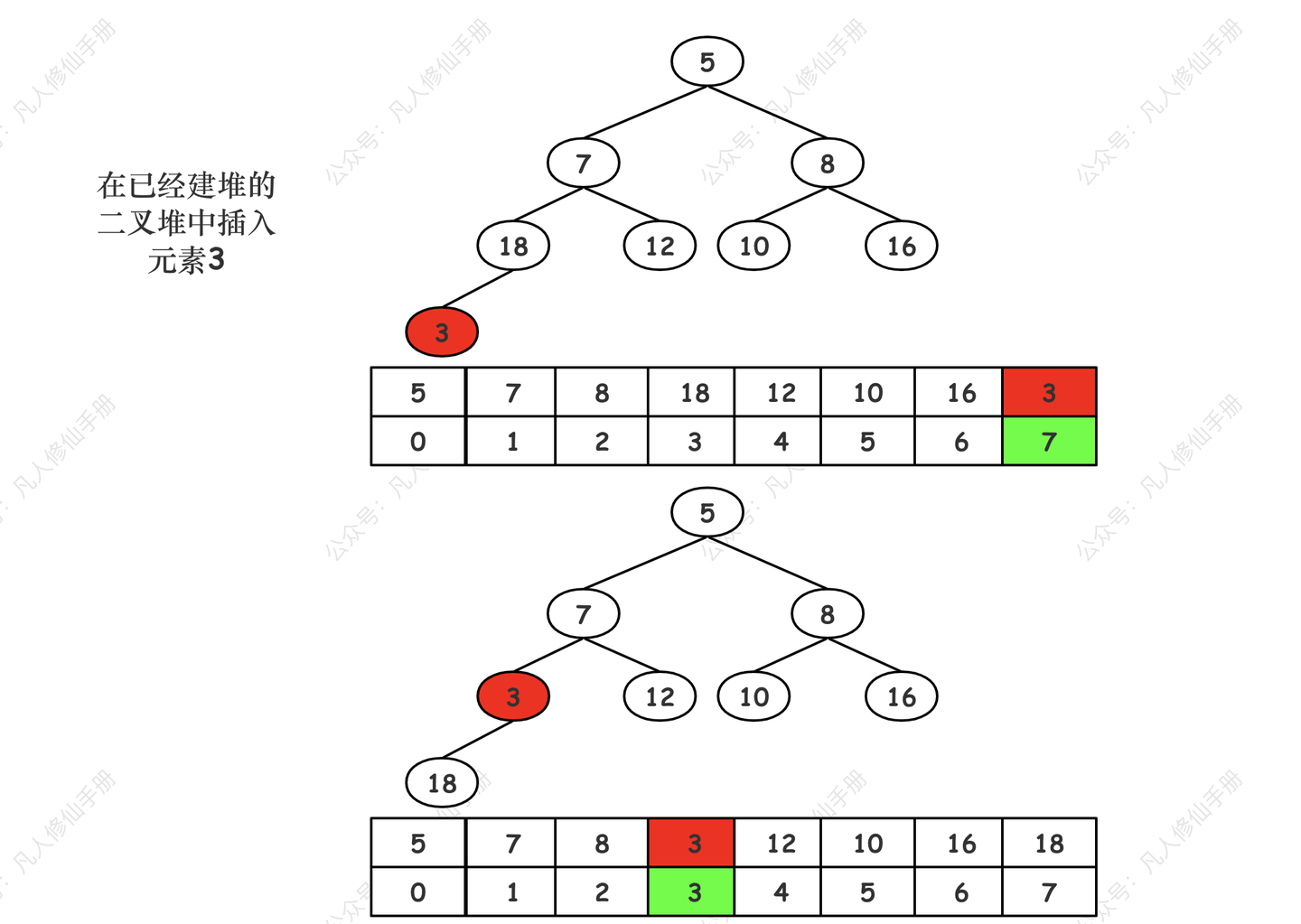
插入元素 3,元素 3 开始上浮
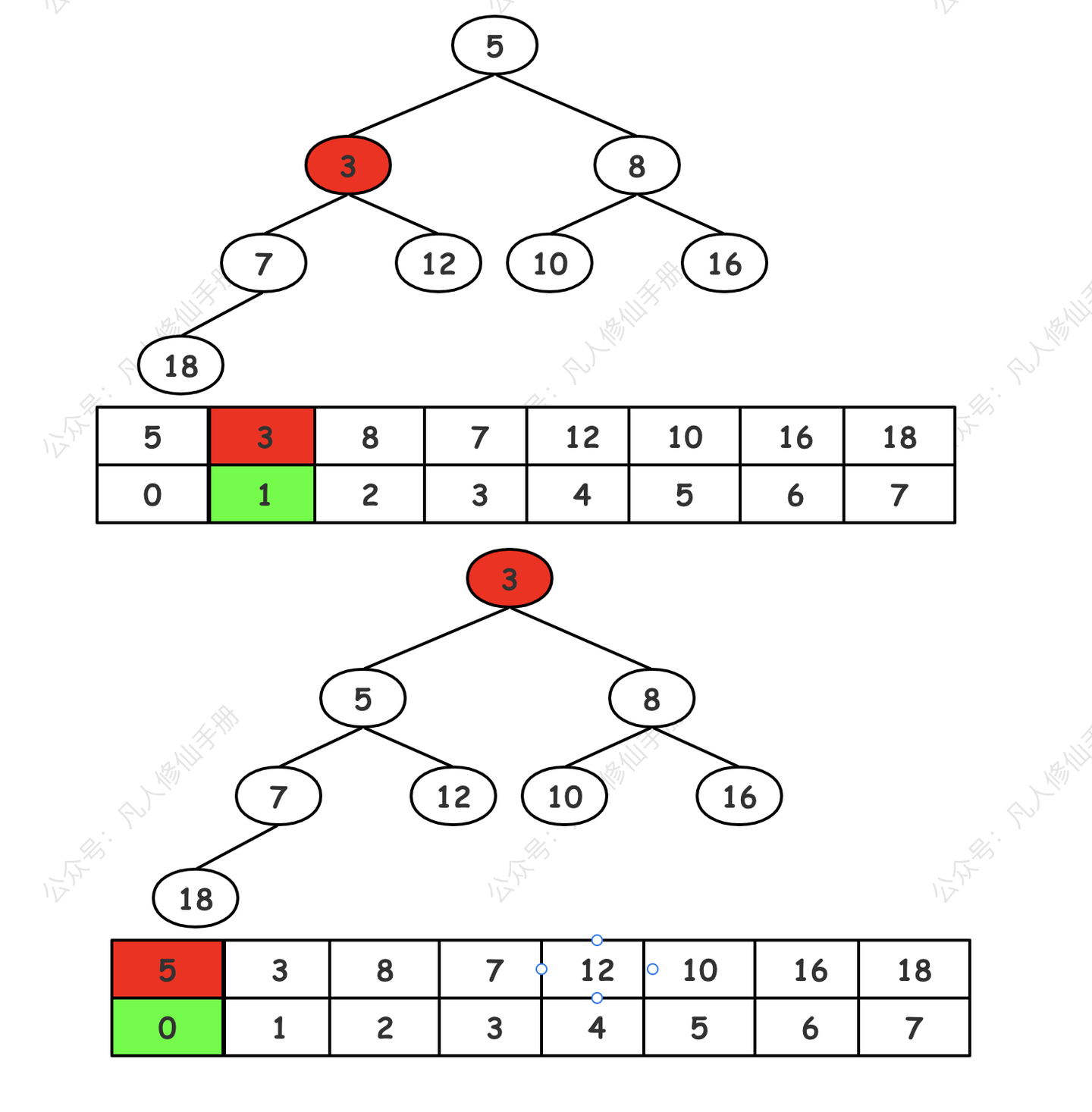
元素 3 继续上浮至根节点
siftDown 原理
siftDown(也称为下沉、下滤或沉下去)通常用于移除操作。在移除堆顶元素后,通常会将堆的最后一个元素移动到堆顶,这可能会违反堆的性质。siftDown 的目的是重新调整元素的位置以恢复堆的性质。
1、过程:
- 在移除堆顶元素后,将堆的最后一个元素移动到堆顶。
- 比较新的堆顶元素与其子节点的值(在最小堆中,父节点的值应小于子节点)。
- 如果新堆顶的值大于任一子节点的值,则它与其最小的子节点交换位置。
- 继续向下比较和交换,直到新堆顶的值小于其所有子节点,或者它已经成为叶节点。
2、目的:
- 确保在移除堆顶元素后,堆仍然保持最小堆(或最大堆)的性质。
以最小堆为例 展示 siftDown () 操作
从最后一个非叶子节点开始,沿着树重复降级直到它小于或等于其子项或者是叶子来保持堆不变性
siftDown 演示
第一步,从第一个非叶子节点 index 为 2 值为 8 开始,执行 siftDown。
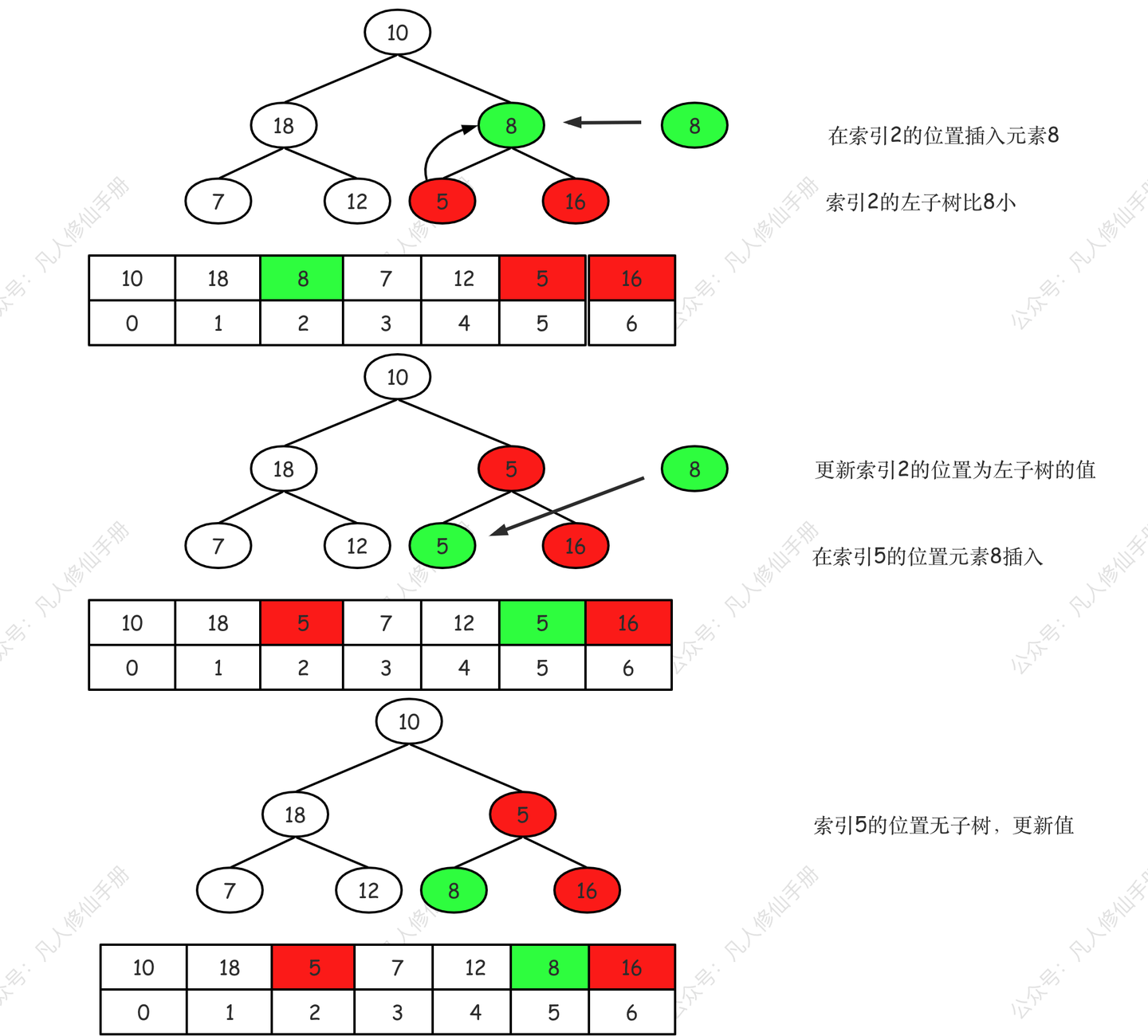
第二步,index 为 1 值为 18,执行 siftDown
 )
)
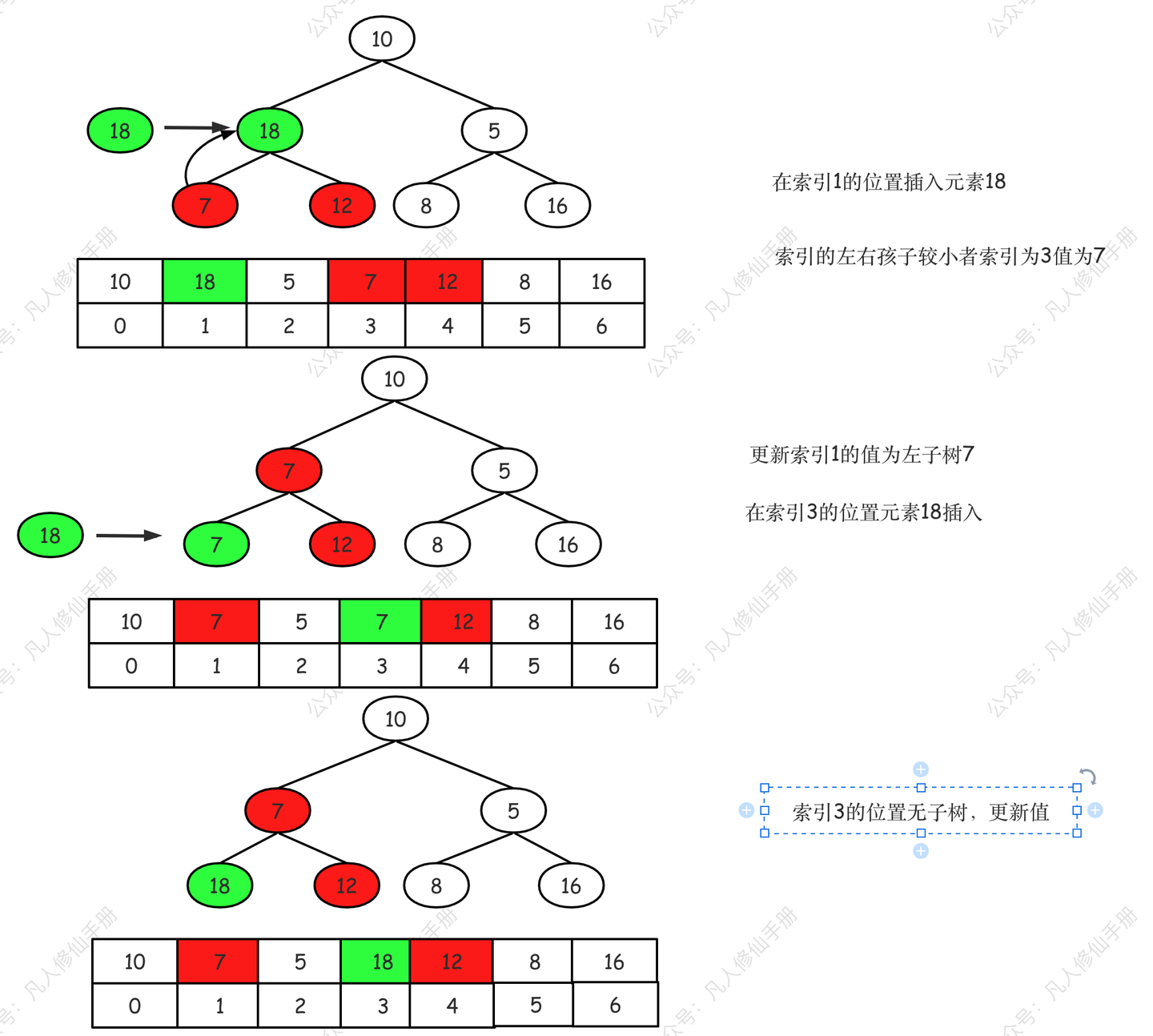
第三步,index 为 0 值为 10,执行 siftDown
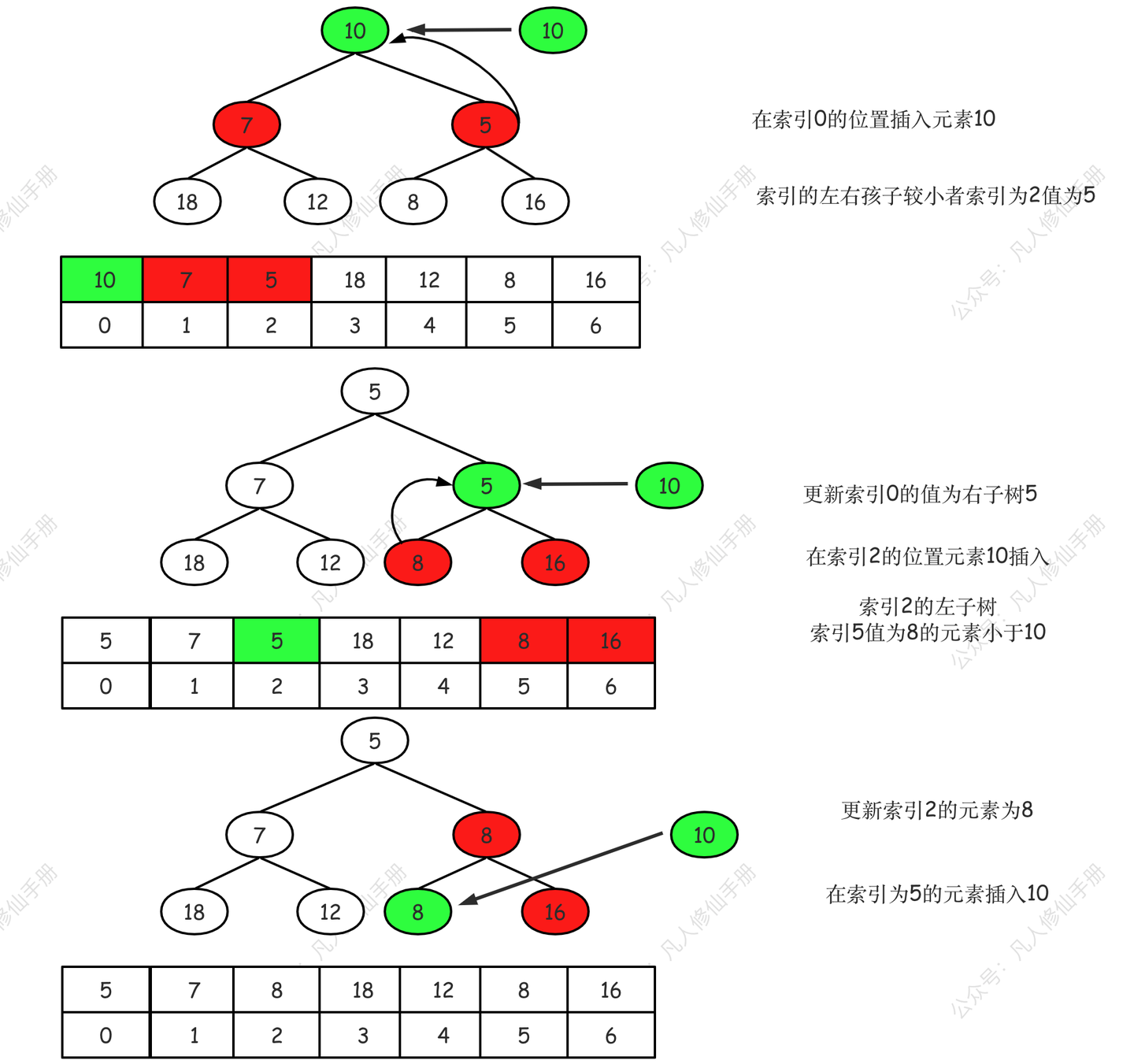

siftDown 源码
在位置 k 处插入项 x,通过将 x 沿着树重复降级直到它小于或等于其子项或者是叶子来保持堆不变性。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39/**
* 在位置 k 处插入项 x,通过将 x 沿着树重复降级直到它小于或等于其子项或者是叶子来保持堆不变性。
*/
private static <T> void siftDownComparable(int k, T x, Object[] es, int n) {
// assert n > 0;
Comparable<? super T> key = (Comparable<? super T>) x;
int half = n >>> 1; // loop while a non-leaf
// 将 x 沿着树重复降级直到它小于或等于其子项或者是叶子来保持堆不变性。
while (k < half) {
// 记录两个孩子节点中的较小节点
int child = leftChild(k); // assume left child is least
// 记录 两个孩子节点中的较小者
Object c = es[child];
// 右边孩子节点
int right = child + 1;
// 右边孩子节点存在 并且 左边孩子节点大于右边孩子节点 寻找两个孩子节点中的较小者
if (right < n &&
((Comparable<? super T>) c).compareTo((T) es[right]) > 0)
// 更新孩子节点和索引
c = es[child = right];
// key小于两个孩子节点 满足堆的性质
if (key.compareTo((T) c) <= 0)
break;
es[k] = c;
// 下一轮开始 孩子节点比较
k = child;
}
// 跳出循环 在位置 k 处插入项 x,
es[k] = key;
}
private static int leftChild(int k) {
return (k << 1) + 1;
}
这两种操作都是为了维护堆的根本性质:在最小堆中,每个父节点的值都小于或等于其子节点的值;在最大堆中,则每个父节点的值都大于或等于其子节点的值。通过 siftUp 和 siftDown,无论是在添加新元素还是在移除元素后,堆都能有效地重新调整以保持其结构和性质。
Heapfy 堆化操作
将数组进行排序,使其具备二叉堆的性质。 堆化(Heapify)是一种将给定数组转换为堆结构的过程。这个操作是构建堆(特别是在进行堆排序时)的核心。堆化可以用于构建最大堆或最小堆。这里以最小堆为例来说明堆化操作的步骤:
- 理解堆的数组表示:在堆的数组表示中,对于任意位于索引 i 的节点,其左子节点位于
2 * i + 1,右子节点位于2 * i + 2,父节点位于(i - 1) / 2(假设数组索引从 0 开始)。 - 找到最后一个非叶子节点:堆化过程从最后一个非叶子节点开始,向数组的起始位置遍历。在一个大小为 n 的数组中,最后一个非叶子节点的位置是
(n / 2) - 1。 - 向下调整(Sift Down):对于每个非叶子节点,执行向下调整的操作。这包括比较节点与其子节点的值,并在必要时交换它们的位置,以确保父节点的值大于子节点(在最大堆中)。
- 比较当前节点(假设索引为 i)的值与其左右子节点的值。
- 如果左子节点或右子节点的值大于当前节点的值,则将其与值最大的子节点交换。
- 继续向下调整,直至到达叶子节点或当前节点的值大于其子节点。
反复进行向下调整:从最后一个非叶子节点开始向上,对每个非叶子节点重复进行向下调整的过程,直到处理完数组的第一个元素。
通过这个过程,可以将任意数组转换成最大堆。同样的方法可以应用于构建最小堆,唯一的区别是在向下调整时确保父节点的值小于子节点的值。
堆化操作是构建堆和进行堆排序的关键步骤,它使得可以在 O (n) 的时间复杂度内将无序数组转换成堆结构,为高效的元素插入和删除提供了基础。
从最后一个非叶子节点开始(int i = (n>>>1) - 1 ),从后往前做 siftDown () 操作1
2
3
4
5
6
7
8
9
10/**
* 将一个数组构建成堆
*/
private void heapify() {
final Object[] es = elementData;
int n = size;
int i = (n >>> 1) - 1;
for (; i >= 0; i--)
siftDownComparable(i, (E) es[i], es, n);
}
最小堆的基础数据组成1
2
3
4
5
6
7public static final int SOFT_MAX_ARRAY_LENGTH = Integer.MAX_VALUE - 8;
// 1+2+4+8
private static final int DEFAULT_INITIAL_CAPACITY = 15;
transient int size = 0;
//用来存放数据
private Object[] elementData;
最小堆的构造函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68public ComparableArrayMinHeap() {
this(DEFAULT_INITIAL_CAPACITY);
}
public ComparableArrayMinHeap(int initialCapacity) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.elementData = new Object[initialCapacity];
}
/**
* 将一个数组堆化处理
*
* @param data 带堆化的数组
*/
public ComparableArrayMinHeap(E[] data) {
initFromArray(data);
}
private void initFromArray(E[] data) {
initElementsFromArray(data);
heapify();
}
/**
* 初始化堆的内存
*
* @param data 初始化传入的树组
*/
private void initElementsFromArray(E[] data) {
int len = data.length;
for (Object e : data)
if (e == null)
throw new NullPointerException();
// 确保已经初始化
this.elementData = ensureNonEmpty(data);
this.size = len;
}
/**
* Establishes the heap
*/
private void heapify() {
final Object[] es = elementData;
// 容量
int n = size;
//
int i = (n >>> 1) - 1;
for (; i >= 0; i--)
siftDownComparable(i, (E) es[i], es, n);
}
private static int leftChild(int k) {
return (k << 1) + 1;
}
private static int rightChild(int k) {
return (k << 1) + 2;
}
private static int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException("index-0 doesn't have parent");
}
return (index - 1) >>> 1;
}
二叉堆中插入元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38public boolean add(E e) {
return offer(e);
}
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
int i = size;
if (i >= elementData.length)
grow(i + 1);
siftUp(i, e);
size = i + 1;
return true;
}
/**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
private void grow(int minCapacity) {
int oldCapacity = elementData.length;
// Double size if small; else grow by 50%
int newCapacity = newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
oldCapacity < 64 ? oldCapacity + 2 : oldCapacity >> 1
/* preferred growth */);
elementData = Arrays.copyOf(elementData, newCapacity);
}
查看二叉堆堆顶元素1
2
3public E peek() {
return (E) elementData[0];
}
取出二叉堆堆顶元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18public E poll() {
final Object[] es;
final E result;
if ((result = (E) ((es = elementData)[0])) != null) {
final int n;
// 数组的最后一个元素
final E x = (E) es[(n = --size)];
// help gc
es[n] = null;
if (n > 0) {
// 将数组的最后一位元素放入堆顶 然后执行siftDown
siftDownComparable(0, x, es, n);
}
}
return result;
}
Tips**
在 Java 中,>>> 和 >> 都是位运算符,用于对整数类型的操作数执行位移操作。不过,这两个运算符在处理符号位时的行为有所不同,这是它们之间的主要区别。
右移运算符 (>>)
- 这是一个带符号的右移运算符。
- 它将操作数向右移动指定的位数。
- 在左侧空出的位上填充原始数的最高位(符号位)。如果原始数是正数,则在左侧填充 0;如果是负数,则在左侧填充 1。
- 这意味着 >> 保留了操作数的符号。
无符号右移运算符 (>>>)
- 这是一个无符号的右移运算符。
- 它也将操作数向右移动指定的位数。
- 不同的是,无论原始数的符号如何,在左侧空出的位上总是填充 0。
- 这意味着 >>> 不保留操作数的符号,对于正数和负数的处理方式是一样的。
运算符示例
为了更好地理解这两个运算符的区别,让我们看一些具体的例子。假设我们有一个 8 位的整数(为了简单起见,使用 8 位而不是 Java 中的 32 位或 64 位)。1
2
3
4
5
6
7
8
9
10int a = 5; // 二进制表示: 00000101
int b = -5; // 二进制表示: 11111011 (在8位系统中)
// 使用 >> 运算符
System.out.println(a >> 1); // 结果是 2,二进制表示: 00000010
System.out.println(b >> 1); // 结果是 -3,二进制表示: 11111101
// 使用 >>> 运算符
System.out.println(a >>> 1); // 结果是 2,二进制表示: 00000010
System.out.println(b >>> 1); // 结果是一个很大的正数
在上面的例子中,对于正数 a,>> 和 >>> 的结果相同。但对于负数 b,>> 保留了符号位,而 >>> 通过在左侧填充 0,得到了一个很大的正数。由于 Java 使用补码表示负数,-5 的补码是 11111011,使用 >>> 之后变成了 01111101,这是一个很大的正数。
总之,>> 是带符号的右移,它保留了数字的符号,而 >>> 是无符号的右移,不考虑符号位。在处理负数时,这两者的差异尤为明显。
第一个非叶子节点
为了理解 (n>>> 1) - 1 这个表达式是如何计算出最后一个非叶子节点的,我们需要先理解堆(作为一种完全二叉树)的一些性质。
在一个完全二叉树中:
- 如果树的总节点数为 n,那么叶子节点的数量大致为 n / 2(或稍微多一点,取决于 n 是奇数还是偶数)。
- 最后一个非叶子节点是第一个有叶子节点的节点,从而是最后一个叶子节点的父节点。
现在来看 (n>>> 1) - 1 这个表达式:
- >>> 是 Java 中的无符号右移操作符。它将数字向右移动指定的位数。在这种情况下,n >>> 1 相当于将 n 除以 2(向下取整),得到大约一半的节点数量。
- 因为数组索引从 0 开始,所以需要减去 1 来得到最后一个非叶子节点的正确索引。
例如,假设堆有 7 个节点(索引为 0 到 6):
- 叶子节点是索引 3、4、5、6(总共 4 个,即 7 的一半)。
- 最后一个非叶子节点是索引 2(3 的父节点),这也是 (7>>> 1) - 1 = 3 - 1 = 2 的结果。
因此,这个表达式是一种快速而有效的方式来找到在堆(作为一个数组表示的完全二叉树)中最后一个非叶子节点的索引。