《Binary Search Tree BST 二叉搜索树》

《算法与数据结构:Binary Search Tree BST 二叉搜索树》
简介
二分搜索树(Binary Search Tree,简称 BST)是一种基于二叉树的数据结构,它在数据存储、检索和管理方面具有独特的优势。每个节点都有一个键(和相应的值)及最多两个子节点。它的关键特性是,对于树中的任意节点 X,其左子树中的所有键都小于 X 的键,而右子树的键都大于 X 的键。这一特性使得二分搜索树在执行查找、插入和删除操作时效率较高,是许多高级数据结构和算法的基础。
定义和特性
- 定义:二分搜索树是一个二叉树,其中每个节点都含有一个可比较的键(及与之关联的值),并且对于任何节点,其左子树中的所有键都小于该节点的键,其右子树的所有键都大于该节点的键。
- 特性:
- 有序性:通过中序遍历二分搜索树,可以获得一个有序的键序列。
- 动态数据结构:二分搜索树可以在运行时动态地插入和删除节点,从而适应数据集的变化。
- 效率:在平衡的情况下,二叉搜索树的操作(如查找、插入、删除)可以在 O (log n) 时间内完成,其中 n 是树中的节点数。
节点结构
每个节点通常包含以下几个基本组成部分:
- 键(Key):节点的唯一标识符,用于节点间的比较。
- 值(Value):与键相关联的数据。
- 左子节点(Left Child):指向左侧子节点的指针,该子节点的键小于当前节点。
- 右子节点(Right Child):指向右侧子节点的指针,该子节点的键大于当前节点。
二叉搜索树是一种特殊的二叉树,它满足以下条件:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 左右子树也必须是二叉搜索树。
- 不存在两个节点具有相同的值。
二分搜索树与普通二叉树的区别
虽然二分搜索树是基于二叉树的,但它通过节点间键值的有序关系增加了额外的结构性,这使得二分搜索树在执行查找、插入和删除等操作时更为高效。相比之下,普通的二叉树不强制要求节点之间遵循特定的顺序,这可能导致上述操作的效率较低。
基本操作
- 查找:从根节点开始,递归或循环地比较当前节点的键与目标键,根据比较结果转向左子树或右子树。
- 插入:从根节点开始,找到合适的叶子节点位置插入新节点,以保持二叉搜索树的有序性。
- 删除:删除操作稍复杂,分三种情况:删除的节点是叶子节点、只有一个子节点、有两个子节点。
- 遍历:常见的遍历方式包括中序遍历(In-order),前序遍历(Pre-order)和后序遍历(Post-order)。中序遍历二叉搜索树会按键的升序访问所有节点。
构建二分搜索树
基础元素 Node
1 | static class Node<K, V> { |
构造函数
1 | private Node<K, V> root; |
插入操作
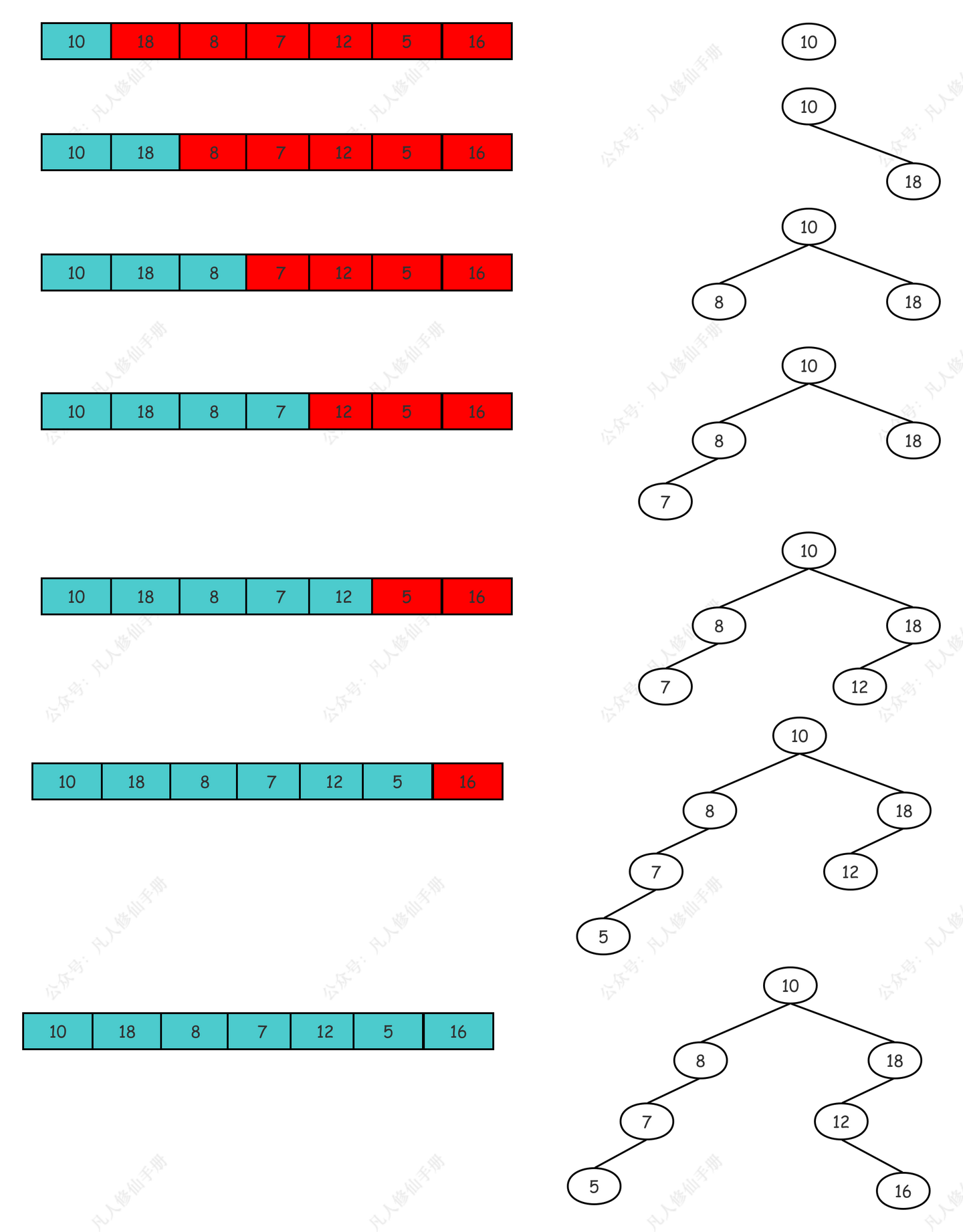
在二分搜索树中插入一个新节点的过程涉及到比较新节点的键与当前节点键的大小,以决定是将新节点插入到当前节点的左侧还是右侧。
- 步骤:
- 从根节点开始,比较新节点的键与当前节点的键。
- 如果新节点的键小于当前节点的键,则向左子树递归;如果大于,则向右子树递归。
- 如果当前节点的相应子树为空,则在这个位置插入新节点。
1
2
3public void add(K key, V value) {
root = add(root, key, value);
}
方法签名:向一颗二分搜索树中添加一个元素,并返回添加元素后的二分搜索树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19/**
* 向以node为根的二分搜索树中添加键值对key value
* 返回插入新结算后二分搜索树的根
*/
private Node<K, V> add(Node<K, V> node, K key, V value) {
if (node == null) {
++size;
return new Node<K, V>(key, value);
}
if (key.compareTo(node.key) < 0) {
return node.left = add(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
return node.right = add(node.right, key, value);
} else {
// key.compareTo(node.key) = 0 update
node.value = value;
return node;
}
}
删除操作
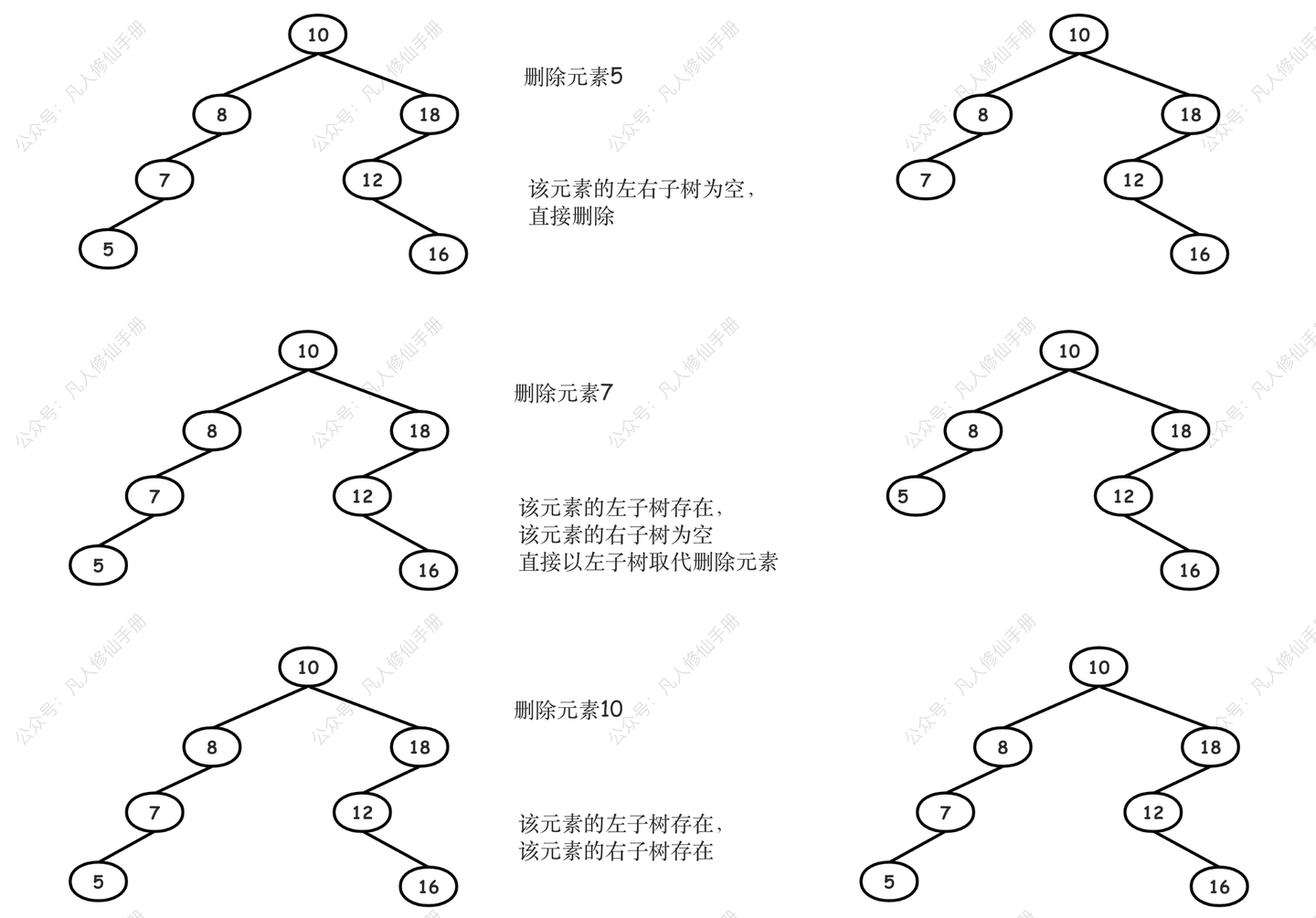
删除操作是二分搜索树中最复杂的操作之一,特别是当需要删除的节点既有左子树又有右子树时。
- 删除叶子节点:直接将父节点指向该叶子节点的链接设为 null。
- 删除只有一个孩子的节点:将该节点的父节点指向该节点的唯一子节点。
- 删除有两个孩子的节点:
- 找到该节点右子树中的最小节点(或左子树中的最大节点)。
- 用这个最小节点的键和值替换要删除的节点。
- 删除原最小节点。

1
2
3
4
5
6
7
8
9
10
11
12/**
* 从二分搜索树中删除键为key的节点
*/
public V remove(K key) {
Node<K, V> removeNode = getNode(root, key);
if (removeNode != null) {
root = remove(root, key);
return removeNode.value;
} else {
return null;
}
}
方法签名:删除二叉树 Node 中的 key,并返回删除后的 Node 二叉树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37/**
* @param node 二叉树
* @param key 要移除的Key
* @return 移除Key节点后的的二叉树
*/
private Node<K, V> remove(Node<K, V> node, K key) {
if (node == null) {
return null;
}
if (key.compareTo(node.key) < 0) {
node.left = remove(node.left, key);
return node;
} else if (key.compareTo(node.key) > 0) {
node.right = remove(node.right, key);
return node;
} else {
//key.compareTo(node.key) = 0
if (node.left == null) {
Node<K, V> rightNode = node.right;
node.right = null;
size--;
return rightNode;
} else if (node.right == null) {
Node<K, V> leftNode = node.left;
node.left = null;
size--;
return leftNode;
} else {
Node<K, V> successor = minimum(node.right);
successor.left = node.left;
successor.right = remove(node.right, successor.key);
node.left = node.right = null;
return successor;
}
}
}
常规方法
1 | /** |
二叉树的遍历
遍历二分搜索树是访问树中每个节点的过程,以特定的顺序执行操作(如打印节点值)。遍历对于理解树的结构、调试代码和实现树的算法至关重要。
前序遍历 preOrder
前序遍历首先访问根节点,然后递归地对左子树和右子树进行前序遍历。这种遍历方式适用于创建树的副本或打印树的结构。1
2
3
4
5
6
7
8
9
10
11
12public void preOrder() {
preOrder(root);
}
private void preOrder(Node<K, V> root) {
if (root == null) {
return;
}
System.out.println(root.key);
preOrder(root.left);
preOrder(root.right);
}
使用栈实现非递归的前序遍历
- 创建一个空栈。
- 将根节点压入栈中。
- 当栈不为空时,执行以下操作:
- 弹出栈顶元素,访问该元素。
- 将弹出节点的右子节点(如果有)压入栈中。
- 将弹出节点的左子节点(如果有)压入栈中。
注意,右子节点先入栈,左子节点后入栈,这样可以保证左子节点先被访问。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public void preOrderNR() {
if (root == null) {
return;
}
Deque<Node<K, V>> stack = new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()) {
Node<K, V> node = stack.pop();
System.out.println(node.key);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
中序遍历 inOrder
中序遍历首先递归地对左子树进行中序遍历,然后访问根节点,最后递归地对右子树进行中序遍历。中序遍历二分搜索树可以得到一个有序的键序列,是二分搜索树最常用的遍历方式。1
2
3
4
5
6
7
8
9
10
11
12public void inOrder() {
inOrder(root);
}
private void inOrder(Node<K, V> root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.println(root.key);
inOrder(root.right);
}
使用栈实现非递归的中序遍历
1 | public void inOrderNR() { |
后序遍历 postOrder
后序遍历首先递归地对左子树和右子树进行后序遍历,然后访问根节点。后序遍历适用于递归释放或删除树的节点,因为它确保节点在其子节点被处理后才被访问。1
2
3
4
5
6
7
8
9
10
11
12public void postOrder() {
postOrder(root);
}
private void postOrder(Node<K, V> root) {
if (root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.println(root.key);
}
使用栈实现非递归的后序遍历
1 | public void postOrderNR() { |
层序遍历
层序遍历(广度优先搜索)按照树的层次从上到下遍历树的节点,通常使用队列来实现。层序遍历用于寻找最短路径、进行层次分析或在树中按层次顺序执行操作。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17public void levelOrder() {
if (root == null) {
return;
}
Queue<Node<K, V>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node<K, V> node = queue.poll();
System.out.println(node.key);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
二分搜索树以其独特的结构和操作效率,在众多领域内发挥着重要作用。以下是一些主要的应用场景:
构建动态数据结构
二分搜索树能够动态地插入和删除节点,使其成为实现各种动态数据结构(如集合、映射和优先队列)的理想选择。通过二分搜索树,可以在对数时间内完成添加、查询和删除等操作,大大提高了数据处理的效率。
实现查找表
二分搜索树特别适合用于实现查找表,其中包括键值对的存储和检索。由于其有序性,二分搜索树可以快速定位到一个键,并检索或更新与之关联的值。这在数据库管理系统和文件系统中尤其有用。
算法中的应用
在算法设计中,二分搜索树用于解决诸如范围查询、排序和近似匹配等问题。例如,通过中序遍历二分搜索树,可以高效地实现数据的排序。此外,二分搜索树也常用于实现各种高级算法,如动态顺序统计、区间树和伸展树等。
支持范围操作
二分搜索树支持高效的范围搜索操作,可以快速找到给定范围内的所有键。这在需要对数据进行分段分析或查询特定区间内的数据时特别有用,如在报告生成和数据分析应用中。
高级话题和优化
虽然标准的二分搜索树在许多情况下表现良好,但在最坏情况下它可能会退化成一个链表,导致操作效率大幅下降。为了解决这个问题,研究人员提出了多种平衡二叉搜索树,如 AVL 树、红黑树和 B 树等。这些树通过在树操作中加入旋转和重组操作,保证了树的平衡性,从而确保了操作的最坏情况时间复杂度为对数级别。此外,二分搜索树的性能也可以通过各种优化策略,如节点缓存、懒惰删除和树的重构等,进一步提高。