Nadav's 算法之旅

《算法与数据结构：优先队列 PriorityQueue》

什么是优先队列？

优先队列是一种特殊的队列，其核心特性在于队列中的元素是按照一定的优先级进行排序的，而不是按照它们进入队列的顺序。在优先队列中，元素被赋予一个优先级，当访问队列时，优先级最高的元素最先被删除。这种机制使得优先队列非常适用于那些需要快速访问最重要元素的场合。

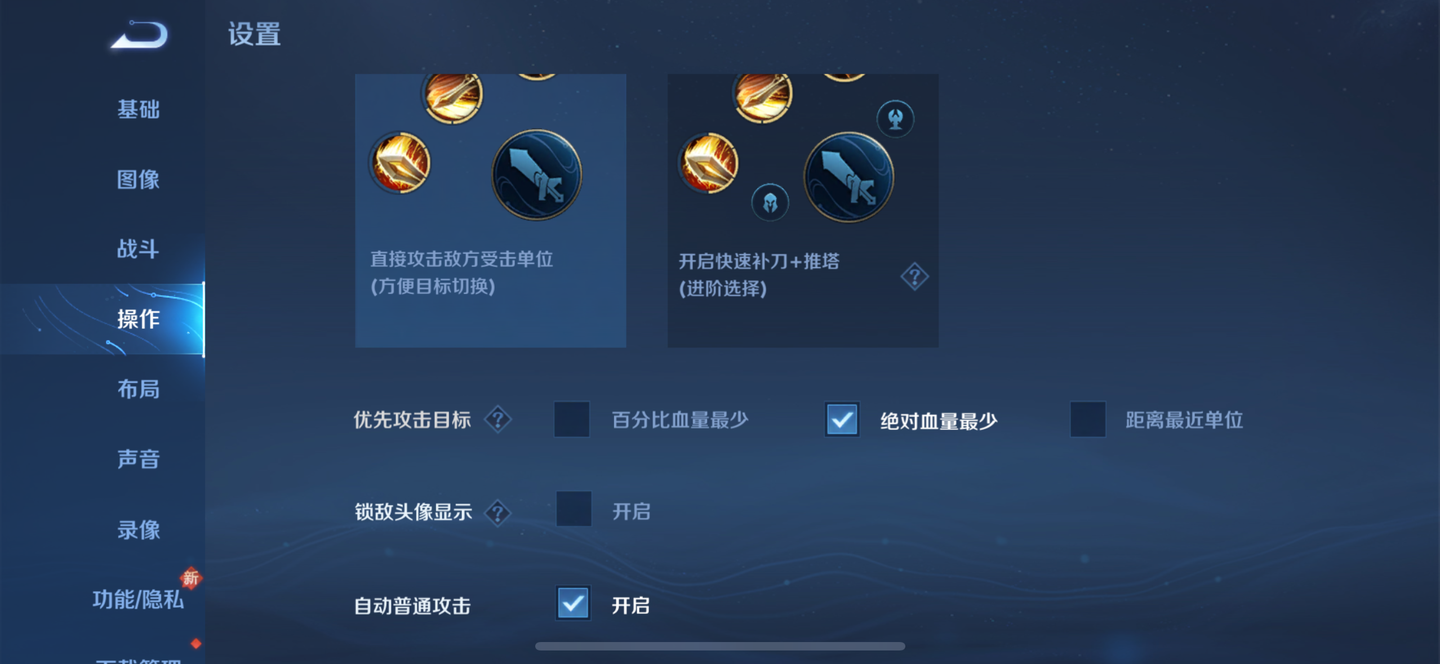
可以看到优先攻击目标有三个选项，当我们点击自动补刀时，游戏英雄就会按照相应的优先级进行攻击

特点

• 动态排序：优先队列内部的元素会根据它们的优先级动态排序，确保每次出队的都是当前优先级最高的元素。
• 高效性：通过使用高效的数据结构（如二叉堆），优先队列可以在对数时间复杂度内完成插入和删除最优元素的操作。

应用场景

• 任务调度：在操作系统中管理进程或任务的执行顺序。
• 图算法：如在 Dijkstra 最短路径算法中选择下一个要访问的节点。
• 事件驱动模拟：按事件优先级顺序处理模拟事件。

《算法与数据结构：Heap》

堆

堆是一种数据结构，它是一种完全二叉树，具有以下特点：

1. 堆是完全二叉树，即每个节点都有两个子节点。
2. 堆是一种有序树，即对于任意节点 n，如果 n 有左子节点 l 和右子节点 r，则 n 的值比 l 和 r 的值都大或都小。
3. 堆可以分为最大堆和最小堆两种，最大堆的根节点是堆中最大的元素，最小堆的根节点是堆中最小的元素。

《算法与数据结构：排序算法纲领》

排序算法概览

排序算法的概念

排序算法是一类算法，用于将一组数据元素（通常是数组）按照特定的顺序（如升序或降序）重新排列。排序是计算机科学中基本的操作之一，广泛应用于数据处理、数据库系统、算法设计等领域。

排序算法的本质

排序算法的本质是比较和交换（或移动）数据元素，以达到预定的顺序。这个过程通常涉及以下基本操作：

• 比较：判断两个元素之间的顺序关系。
• 交换 / 移动：将元素置于正确的位置，确保它们符合排序顺序。
• 迭代 / 递归：重复执行比较和交换 / 移动步骤，直到整个序列有序。

《算法与数据结构：Tree 的基本概念》

树的基本概念

树（Tree）结构简介

树是一种层级数据结构，非常适合用来表示具有层级关系或者需要快速搜索操作的数据集合。它由节点 Nodes 组成，这些节点通过边 Edges 相连。一个树结构有以下特点：

• 树与子树：树是一个有限集合，子树则是该集合的子集。就像套娃一样，一棵树下面还包含着其子树。比如，树 T1 的子树为 树 T2、T3、T4，树 T2 的子树为 T5、T6。 上图中还有许多子树没有标记出来 。
• 结点 (Node)：一个结点包括一个数据元素和若干指向其子树分支。比如，在树 T1 中，结点 A 包括一个数据元素 A 和 三个指向其子树的分支。上图中共有 18 个结点 。
• 根结点 (Root)：一颗树只有一个树根，这是常识。在数据结构中，“树根” 即根节点。比如，结点 A 是树 T1 的根结点；结点 C 是树 T1 的子结点，是树 T3 的根结点。
• 度 (Degree)：一个结点拥有的子树数。比如，结点 A 的度为 3，结点 G 的度为 2，结点 H 的度为 1。
• 叶子 (Leaf)/ 终端结点：度为 0 的结点被称为叶子结点，很形象。比如对于树 T1 来说，结点 F、K、L、M、N、O、P、Q、R 均为叶子节点。
• 分支结点 / 非终端结点：和叶子结点相对，即度不为 0 的结点。
• 内部结点：顾名思义在树内部的结点，即不是根结点和叶子结点的结点。
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点。如上图，A 是 B 的父节点。
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点。 如上图，B 是 A 的孩子节点。
• 兄弟节点：具有相同父节点的节点互称为兄弟节点。 如上图，B、C 是兄弟节点。
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟节点。如上图，E、F、G、H 互为堂兄弟节点。
• 节点的祖先：从根到该节点所经分支上的所有节点。如上图，A 是所有节点的祖先。
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图，所有节点都是 A 的子孙。
• 层次 (Level)：从根结点开始，根为第一层，根的孩子为第二层，依次往下。比如，结点 K 在树 T1 中的层次为 4。
• 深度 (Depth)/ 高度：指树的最大层次。比如，树 T1 的高度为 4 。
• 有序树: 树中任意节点的子结点之间有顺序关系，这种树称为有序树 。
• 无序树 : 树中任意节点的子结点之间没有顺序关系，这种树称为无序树，也称为自由树 。
• 森林：由 m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除，则该树就变成了一片森林，森林中的树由原来根节点的各棵子树构成。

《算法与数据结构：Java 开发者的探索之旅》专栏简介

引言

欢迎来到《算法与数据结构：Java 开发者的探索之旅》一个专为 Java 程序员设计的综合学习平台。无论您是初涉编程世界的新手，还是经验丰富的行业专家，这里都有您需要的知识和资源。通过本专栏，我们将共同探索算法的奥秘和数据结构的精髓，不仅提升您的编程技能，还将激发您解决复杂问题的能力。

第一部分：基础篇

1. 算法和数据结构入门

对于刚开始学习 Java 的读者，我们将从最基本的算法和数据结构开始。这包括了解数组、链表、栈、队列、堆、字典、集合、树等基础数据结构，以及排序和搜索等基本算法。

《算法与数据结构：插入排序算法》

简介

插入排序是一种简单直观的排序算法，它通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实践中对小型数组表现良好，尤其是当数组部分已经排序时。

算法思想

插入排序的基本思想是将待排序的元素看作一个有序表和一个无序表。开始时，有序表中只包含一个元素，而无序表中包含有 n-1 个元素。在排序过程中，每次从无序表中取出第一个元素，将其与有序表中的元素的排序码进行比较，然后将其插入到有序表中的适当位置，形成新的有序表。

关键特点

• 简单直观：易于理解和实现。
• 适用于小型数组：对于小数据量效率高。
• 稳定排序：相等元素的顺序不会改变。

算法原理

1. 开始排序：从数组的第二个元素开始，这是因为单个元素默认已排序。
2. 选择元素：选择当前元素，与前面的元素进行比较。
3. 寻找位置：如果当前元素小于它前面的元素，则将前面的元素向后移动。
4. 插入元素：重复步骤 3 直到找到当前元素的正确位置，然后将它插入。
5. 重复过程：对数组中的每个未排序元素重复步骤 2-4。
6. 完成排序：当所有元素都被考虑过，数组排序完成。

《算法与数据结构：冒泡排序算法》

冒泡排序算法

算法简介

冒泡排序是一种简单的排序算法，它重复地遍历待排序的元素列表，比较相邻的元素，并在需要时交换它们的位置。每遍历一次列表，至少有一个元素会被移至其正确的位置，这个过程类似于气泡从水底升到水面的过程，因此得名 “冒泡排序”。

关键特点

• 简单直观：易于理解和实现。
• 效率较低：对于大量元素的列表，其性能不如更复杂的排序算法。
• 稳定性：相等的元素在排序后保持原有顺序。

算法工作原理

• 比较和交换：从列表的开始处开始，比较相邻的两个元素，如果它们的顺序错误就把它们交换过来。
• 重复过程：对列表的每一对相邻元素执行步骤 1，直到列表的末尾。这完成了列表的一次完整遍历。
• 重复遍历：重复步骤 1 和 2，每次遍历都会减少最后一个比较的元素。
• 完成排序：当没有更多元素需要比较时，列表排序完成。

《算法与数据结构：选择排序算法》

选择排序算法

简介

选择排序是一种简单直观的排序算法。它的工作原理是每次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。选择排序是不稳定的排序方法（即相同的元素可能在排序后的序列中有不同的顺序）。

算法原理

选择排序算法的主要步骤如下：

1. 在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置。
2. 从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。
3. 重复第二步，直到所有元素均排序完毕。

《算法与数据结构：Node》

节点（Node）数据结构基石

理解 Node 数据结构及其应用

Node（节点）在计算机科学中扮演着核心角色，它是构建更复杂数据结构的基石。深入理解 Node 及其在各种数据结构中的应用，对于开发高效、可扩展的软件应用至关重要。

Node 节点概念

• 定义与结构：Node 通常是一个包含数据和指向其他节点的引用的对象。它的结构可能因应用的不同而有所不同，但通常包括至少一个数据字段和一个或多个链接字段。
• 类型：
  • 单链表节点：包含数据和指向下一个节点的单个链接。
  • 双链表节点：除了指向下一个节点的链接外，还有指向前一个节点的链接。
  • 树节点：包含多个链接，通常指向其子节点。
  • 图节点：可以有多个链接，指向多个其他节点，表示图中的边。

《算法与数据结构：手写 ArrayList》

List 的数组

List（列表）是编程中一种极为常见且重要的数据结构，用于存储元素的有序集合。在 Java 中，List 是一个接口，它允许我们以线性方式存储元素，同时提供了一系列操作这些元素的方法，List 是线性表的一种。

线性表是一种最基本、最简单、也是最常用的一种数据结构。一个线性表是 n 个具有相同特性的数据元素的有限序列。在这些元素中，每个元素都有一个前驱和一个后继，除了第一个和最后一个元素之外，其它元素都是首尾相接的。

List 数据结构的基本概念

• 定义：List 是一种允许重复元素的序列，它可以维护元素插入的顺序。
• 特点：
  • 动态大小：List 的大小不是固定的，它可以根据需要增长或缩小。
  • 有序集合：每个元素都有其特定的位置（索引）。